Soluções da Final das ONI'2018
Problema C - Circuitos elétricos
Tipo de problema: Árvores
Autor do problema: Pedro Paredes (CMU)
Dificuldade do problema: Médio
O Problema
Dado um conjunto de $N$ instruções que descrevem um circuito e um conjunto de $Q$ pares de pilhas, calcular a resistência entre cada par.
Restrições
São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:
| $1 \leq N \leq 100\:000$ | Número de instruções | |
| $1 \leq Q \leq 100\:000$ | Número de pares de pilhas |
Os casos de teste deste problema estão organizados em 6 grupos com restrições adicionais diferentes:
| Grupo | Número de Pontos | Restrições adicionais |
|---|---|---|
| 1 | 10 | $N, Q \leq 15$ |
| 2 | 10 | $N, Q \leq 1 000$, todas as instruções são 'U' ou 'S' |
| 3 | 20 | Todas as instruções são 'U' ou 'S' |
| 4 | 10 | $N, Q \leq 1 000$, todas as instruções são 'U' ou 'P' |
| 5 | 20 | Todas as instruções são 'U' ou 'P' |
| 6 | 30 | - |
Solução Base
Neste problema pedem-nos para calcularmos distâncias num objeto com uma estrutura muito peculiar. Para conseguir resolver este problema é importante conhecer a noção de grafo como estrutura matemática que abstrai um conjunto de entidades e as suas relações. Mas como? Ora, podemos pensar em pilhas e conetores como entidades e as relações entre elas como os fios que as ligam. Para saberem mais sobre este tópico, consultem o guia do Loop apropriado:

Artigo: Introdução a grafos
Este artigo contém uma introdução a grafos.
Tendo o conceito de grafos na cabeça, podemos reescrever o enunciado do problema simplesmente como: dado um grafo sem pesos nas arestas, calcular o caminho mais curto entre dois nós. Este problema é um problema clássico de grafos que pode ser resolvido com um conhecido algoritmo: pesquisa em largura (ou breadth first search, BFS). Este é o tipo de pesquisa em que partindo de um nó visitamos os seus vizinhos, de seguida vizitamos cada um dos seus vizinhos, depois os vizinhos dos vizinhos, etc até atingirmos o nó objetivo, tendo o cuidado de não visitar o mesmo nó duas vezes.

Artigo: Algoritmos em grafos simples
Este artigo introduz vários algoritmos simples para problemas de grafos, incluindo o BFS.
Parece que temos uma solução inicial para o problema, mas o input que nos dão não é exatamente num formato de grafo, são conjuntos de instruções. Se repararem bem, as instruções são definidas de forma recursiva: um circuito é definido à custa de outro que por sua vez é definido à custa de outro e por ai fora seguindo as mesmas regras. Assim, podemos fazer o seguinte: vamos guardar para circuito definido no input o seu terminal positivo (nó mais à esquerda) e o seu terminal negativo (nó mais à direita), ou seja, os nós no grafo que os representam. Agora sempre que um circuito é uma pilha, adicionamos um nó ao nosso grafo e colocamos ambos os terminais iguais a este nó. Se um circuito é em série, adicionamos uma aresta entre o nó que representa o terminal negativo do primeiro circuito e o nó que representa o terminal positivo do segundo. Se um circuito é em paralelo, adicionamos dois novos nós, um como novo terminal positivo e outro como novo terminal negativo, e adicionamos uma aresta entre o nó que representa o terminal negativo de ambos circuitos ao novo terminal positivo e analogamente para o negativo. A imagem seguinte mostra este processo:

Vamos imaginar que já lemos o input e guardamos numa array de nome $tipo\_no[i]$, o tipo do $i$-ésimo nó, e em arrays de nomes $primeiro\_circuito[i]$ e $segundo\_circuito[i]$ a linha onde foram definidos os circuitos que perfazem o circuito $i$ (caso seja em série ou paralelo). Adicionalmente vamos considerar que temos duas funções implementadas: $novo\_no()$, que adiciona um novo nó ao nosso grafo e devolve o seu índice; $adicionar\_aresta(a, b)$, que adiciona uma nova aresta no nosso grafo entre os nós de índices $a$ e $b$. A implementação destas funções é fácil, basta usar uma representação de grafos, como uma lista de adjacências, como referido nos artigos mencionados. Para transformar a lista de instruções num grafo podemos fazer como no código seguinte:
for (i = 0; i < n; i++) {
if (tipo_no[i] == 'U') {
no_esquerda[i] = novo_no();
no_direita[i] = no_esquerda[i];
}
else if (tipo_no[i] == 'P') {
int pc = primeiro_circuito[i];
int sc = segundo_circuito[i];
adicionar_aresta(no_direita[pc], no_esquerda[sc]);
no_esquerda[i] = no_esquerda[pc];
no_direita[i] = no_direita[sc];
}
else if (tipo_no[i] == 'P') {
int pc = primeiro_circuito[i];
int sc = segundo_circuito[i];
no_esquerda[i] = novo_no();
no_direita[i] = novo_no();
adicionar_aresta(no_esquerda[i], no_esquerda[pc]);
adicionar_aresta(no_esquerda[i], no_esquerda[sc]);
adicionar_aresta(no_direita[i], no_direita[pc]);
adicionar_aresta(no_direita[i], no_direita[sc]);
}
}E isto completa a nossa solução mais simples, mas qual a sua complexidade temporal? Ora cada BFS tem complexidade temporal de $O(N)$, pois pode visitar todos os nós até encontrar o nó pretendido. Visto que temos $Q$ pares de nós para processar, esta solução no total tem complexidade $O(NQ)$, o que, se implementada eficientemente, daria para aproximadamente 30 pontos, nomeadamente os grupos onde $N, Q \leq 1 000$.
Solução em série
Vamos assumir agora que o input contém apenas circuitos em série. Não é difícil de ver que neste caso o circuito final será uma linha de pilhas como na imagem seguinte:

Esta imagem corresponde a um dos exemplos do enunciado (o exemplo 2). Também conseguimos observar que a ordem das pilhas depende da ordem em que são definidas nas instruções. Suponhamos que sabemos exatamente a ordem das pilhas na linha de pilhas que representa o circuito, ou seja, no exemplo dado sabemos que a pilha 4 está na posição 1, a pilha 1 na posição 2 e a pilha 6 na posição 4. Neste caso, a distância entre duas pilhas é dada pela distância entre a posição das duas, que é muito fácil de calcular tendo as posições
Só nos falta então calcular a posição das pilhas. A forma mais simples de o fazer é simplesmente percorrer o circuito de cima para baixo e da esquerda para a direita recursivamente. O código seguinte ilustra este procedimento assim como calcular a distância após termos a posição:
int nos = 0; // indice de nos, inicialmente 0
void calcular_posicoes(int circuito) {
if (tipo_no[circuito] == 'U') {
posicao[circuito] = nos++;
return;
}
calcular_posicoes(primeiro_circuito[pos]);
calcular_posicoes(segundo_circuito[pos]);
}
int main() {
// ler input
calcular_posicoes(n - 1); // relembrar: o circuito n-1 e o final
for (int i = 0; i < q; i++) {
// ler pilha1
// ler pilha2
// usamos abs(), ou seja valor absoluto, pois nao sabemos
// qual a pilha com posicao superior
int distancia = abs(posicao[pilha1] - posicao[pilha2]);
// imprimir distancia
}
return 0;
}É fácil de ver que o nosso algoritmo é linear, percorre o circuito completo duas vezes ($O(N)$) e depois efetua uma única operação por cada par de pilhas. No total temos uma complexidade de $O(N + Q)$, mas só funciona para o caso em que o circuito apenas contém ligações em série. Se combinarmos esta solução com a anterior conseguiriamos aproximadamente 50 pontos, visto que conseguiriamos o grupo 3.
Solução ótima
Uma propriedade importante do problema que ainda não explorámos é o facto de a profundidade do circuito ser limitada a 30. Isto indica-nos que deve haver uma forma de calcular distâncias usando apenas a profundidade do circuito.
Podemos tentar imaginar várias formas de aproveitar este facto. Uma delas é que, aparentemente, se a profundidade do circuito for pequena então a distância entre duas pilhas também tem de ser pequena. Infelizmente isto não é verdade (conseguem ver porquê?), por isso teremos pensar noutra forma. Vamos olhar para o circuito como uma árvore. Uma árvore é um tipo muito especial de grafo que não contém nenhum ciclo. Se conhecem o conceito de árvore binária de pesquisa então sabem o que é uma árvore, mas se quiserem aprender mais sobre árvores podem consultar o artigo sobre o assunto:

Artigo: Propriedades básicas de árvores
Este artigo contém uma introdução a árvores.
Claramente um circuito não é uma árvore, visto que as ligações em paralelo induzem ciclos, mas a descrição recursiva de um circuito pode ser representada como árvore. Para o exemplo do enunciado:
U U S 1 2 U P 3 4
Temos a seguinte árvore:
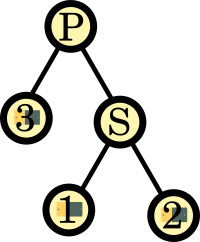
Reparem que colocamos como raiz da árvore o nó relativo ao circuito final, os seus filhos são os dois nós que ele referencia e por ai fora.
Podemos fazer um conjunto de observações. Primeiro, uma pilha é sempre uma folha desta árvore. Sejam $a, b$ duas pilhas da árvore e seja $l$ o seu antecessor comum mais a baixo na árvore, ou seja, o nó de maior profundidade (mais afastado da raiz) que está presente no caminho de $a$ para a raiz e no caminho de $b$ para a raiz. Todos os caminhos entre $a$ e $b$ passam por um terminal de $l$, ou por um terminal do pai de $l$, ou por um terminal do pai do pai de $l$, ... Assim, se calcularmos o caminho mais curto de $a$ e $b$ até cada um desses terminais, a resposta será a menor soma do caminho mais curto de $a$ e $b$ até um dos terminais.
Para isso vamos primeiro ver como calcular a distância de uma pilha $a$ aos terminais do seu pai $p$. Temos dois casos:
- O nó $p$ representa uma ligação em série. Vamos considerar que $a$ é o filho esquerdo de $p$ (o outro caso é análogo). Neste caso a distância ao terminal da esquerda é $0$. Já a distância ao terminal da direita é $1 + c_d$, onde $c_d$ é o "comprimento" do filho direito de $p$, ou seja, a distância de um terminal ao outro desse nó.
- O nó $p$ representa uma ligação em paralelo. Neste caso a distância a cada terminal é exatamente 1.
Notem que podemos precalcular o comprimento de cada nó antes de calcular qualquer distância. Podemos até fazê-lo em tempo linear no tamanho da árvore, basta calcular recursivamente das folhas até à raiz e usar um método semelhante ao anterior para propagar os comprimentos. O seguinte código faz exatamente isto:
void calcular_comprimento(int circuito) {
calcular_comprimento(primeiro_circuito[circuito]);
calcular_comprimento(segundo_circuito[circuito]);
int resposta = 0;
if (node_type[cur] == 'S') {
comprimento[circuito] = 1 + comprimento[primeiro_circuito[circuito]]
+ comprimento[segundo_circuito[circuito]];
}
if (node_type[cur] == 'P') {
comprimento[circuito] = 2 + min(comprimento[primeiro_circuito[circuito]],
comprimento[segundo_circuito[circuito]]);
}
}
// basta chamar calcular_comprimento(n - 1) para preencher a
// array comprimento[] com os valores relevantesTendo calculado a distância de $a$ até aos terminais do seu pai $p$, basta nos ver como obter as distâncias até aos terminais do pai de $p$, ao pai do pai de $p$ e por ai fora. Vamos chamar à distância que já calculámos até ao terminal da esquerda de $p$ de $p_e$ e à distância até ao terminal da direita $p_d$. Vamos então ver como propagar a distância ao pai de um nó. Novamente, temos dois casos:
- O nó relevante representa uma ligação em série. Vamos considerar novamente que o nó de onde viemos é o filho da esquerda do nó relevante. Neste caso a distância ao terminal da esquerda é a mesma $p_e$. Já a distância ao terminal da direita é $p_d + 1 + c_d$.
- O nó relevante representa uma ligação em paralelo. Visto que as distâncias são análogas, vamos calcular apenas a distância ao terminal da esquerda. Um caminho possível que podemos levar é seguir até ao terminal da esquerda do nó filho e depois seguir a ligação ao terminal da esquerda, ou seja, a distância seria $p_e + 1$. Mas podemos também seguir o sentido contrário do ciclo, ou seja, ir até ao terminal direito do nó relevante e depois percorrer o comprimento do seu outro circuito, ou seja, a distância seria $p_d + 2 + c_d + 1$, onde $c_d$ é o "comprimento" do outro circuito filho do nó relevante. O caminho mais curto será o menor destas duas distâncias.
A imagem seguinte ilustra estes dois casos (as cores mostram as diferentes opções de caminhos):
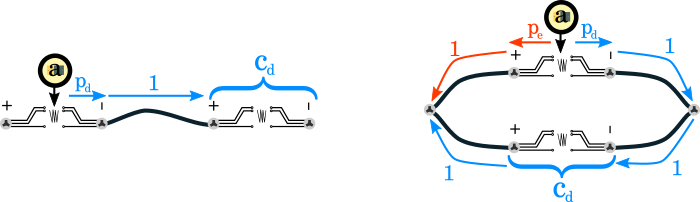
Vamos recapitular o que estamos a fazer: dado um par de pilhas vamos percorrer a árvore que representa o circuito desde cada uma das pilhas (que são folhas) até à raiz (seguindo as ligações de pai de cada nó) e calcular a distâncias até ambos os terminais de cada nó.
Tendo as distâncias a todos estes terminais, como é que as podemos combinar para calcular a distância entre duas pilhas $a$ e $b$? Para todos os nós entre $l$ (o antecessor comum a $a$ e $b$ mais a baixo na árvore) e a raiz, calculamos a soma das distâncias de $a$ e $b$ até ao seu terminal esquerdo, calculamos a soma das distâncias de $a$ e $b$ até ao seu terminal direito e escolhemos o mínimo de todas estas somas. Temos um último caso para considerar, se $l$ for um nó de ligação em série há mais uma maneira de combinar $a$ e $b$. Vamos considerar que $a$ se inclui na sub-árvore esquerda de $l$ e $b$ se inclui na sub-árvore direita de $l$, então podemos ir de $a$ ao terminal direito do filho esquerdo de $l$, seguir o fio que liga os dois filhos de $l$ e depois continuar desde o terminal esquerdo do filho direito de $l$ até $b$. Calculamos o mínimo entre todas estas distâncias e esse mínimo representa a distância entre $a$ e $b$.
Quão boa é esta solução? Além de ler o input temos de precalcular alguma informação, como o comprimento de cada nó (dependendo da implementação, pode ser útil calcular a profundidade de cada nó, mas não é necessário), o que no total tem um custo de $O(N)$. Para cada par de nós, temos de potencialmente percorrer a altura da árvore que representa o circuito. A altura desta árvore é no máximo 30, visto que é a profundidade máxima do circuito segundo o enunciado. Assim, a complexidade desta solução é de $O(N + 30Q)$, o que seria suficiente para os 100 pontos.
Nota final
O que aconteceria se não tivessemos a restrição de profundidade? Será que é possível resolver o problema em tempo melhor que $O(NQ)$? Notem que a nossa solução ótima sem a restrição de profundidade é $O(NQ)$, visto que a profundidade máxima pode ser $O(N)$.
Outra nota importante, o conceito de antecessor mais a baixo na árvore comum a dois nós é um conceito importante conhecido como lowest common ancestor (LCA). Uma operação útil é calcular o LCA de dois nós em tempo sublinear (o mais comum é $\log(N)$). Este é um tópico um pouco mais avançado, mas recorrent. Para mais informação sobre o assunto consultem o artigo relevante:

Artigo: Lowest common ancestor
Este artigo contém uma introdução ao tópico de lowest common ancestor.