Problema C - Torre defeituosa

O Problema

Dado um conjunto de $N$ torres e os cabos que as ligam, determinar a torre defeituosa em menos de $D$ tentativas.

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

1 ≤ $N$ ≤ 100 000	Número de elementos no conjunto
1 ≤ $D$ ≤ $N$	Valores do conjunto

Os casos de teste deste problema estão organizados em 5 grupos com restrições adicionais diferentes:

Grupo	Número de Pontos	Restrições adicionais
1	10	$N$ ≤ 100, $D$ = $N$
2	20	$N$ ≤ 100, $D$ = $N / 2$
3	20	$D$ = 20, as torres formam uma linha
4	25	$N$ ≤ 1  000, $D$ = 12
5	25	$D$ = 20

Soluções Base

O enunciado deste problema é muito simples: é nos dada uma árvore (é importante perceber que o sistema de torres forma uma árvore, visto que é conexo e tem $N$ - 1 ligações, tem de ser uma árvore) e pedem-nos para encontrar um certo nó defeituoso.

Para o primeiro grupo de casos de teste a solução não é difícil. Temos $N$ nós e $D$ tentativas para adivinhar o nó defeituoso, basta adivinharmos todos os nós e eventualmente teremos o nó correto.

Para o segundo teremos de ser ligeiramente mais espertos. Antes de descrevermos a solução final, vamos descrever a solução mais simples possível que evita passar por todos os nós. Se adivinharmos um nó qualquer aleatoriamente e ele não for o correto, o vizinho mais perto do nó defeituoso que nos é dado está, por definição, mais perto do nó defeituoso. Por isso, podemos continuar por adivinhar este nó e de seguida o nó que nos for dado até chegarmos ao nó defeituoso. Esta solução não nos garante que encontramos o nó defeituoso em menos de $N / 2$ tentativas, mas em média é muito melhor do que adivinhar todos os nós. Esta solução passa por todos os nós no caminho entre o primeiro nó que adivinhámos e o nó defeituoso.

Durante a prova, alguns concorrentes conseguiram que a solução anterior passasse o grupo de casos de teste com $D$ = $N / 2$ escolhendo um nó aleatório e, com mais ou menos heurísticas, aplicar a solução anterior. Dado que os casos de teste não eram adversariais e que havia alguma aleatoriedade nos mesmo, a probabilidade de passar os casos de teste escolhendo nós aleatórios era considerável. Ainda assim, era possível arranjar uma solução que garantidamente passa este grupo de casos de teste.

Todos os grafos (ou seja, incluindo as árvores) têm uma noção de diâmetro e centro. O diâmetro de um grafo é a maior caminho entre dois quaisquer nós (que tem, por isso, no máximo $N$ nós), o centro, como o nome indica, é o nó que fica a meio do diâmetro, ou mais formalmente, o nó que minimiza a maior distância a qualquer outro nó. No caso das árvores existem no máximo 2 centros, enquanto que para um grafo geral todos os nós podem ser centros (no grafo completo, por exemplo). O centro de uma árvore está a uma distância de no máximo $N / 2$ de qualquer outro nó, logo podemos aplicar o algoritmo anterior e chegar ao nó defeituoso com no máximo $N / 2$ adivinhas.

Para calcular o centro existem vários algoritmos. Visto que $N$ era menor ou igual a 100, um algoritmo simples que aplica uma pesquisa em profundidade ou largura para calcular a distância entre dois nós podia ser usado para exaustivamente calcular a distância entre cada par de nós com o objetivo de determinar o nó com menor distância até qualquer outro nó (que será o centro). Dependendo da implementação, esta tarefa seria $O(N^3)$ ou $O(N^2)$. O algoritmo mais eficiente para esta tarefa para uma árvore (apenas funciona para árvores) é linear e será abordado nalguns artigos do loop, mas muito brevemente a ideia seria remover todas as folhas da árvore sucessivamente até restarem apenas um ou dois nós, que serão o centro ou bicentro da árvore e podem ser usados como ponto de partida do algoritmo anterior.

Solução Melhorada

O terceiro grupo de casos de teste indica-nos que os nós formam uma linha. Isto simplifica imenso o problema pois o problema fica equivalente a: dado uma sequência de objetos, encontrar um certo objeto especial adivinhando sucessivamente objetos diferentes e recebendo informação sobre para que lado está o objeto especial quando não adivinhamos.

Este problema é exatamente o de procurar um elemento numa lista ordenada, o que nós faz imediatamente lembrar de pesquisa binária. Se mapearmos todos os nós do sistema de torres para uma array, basta-nos aplicar o clássico algoritmo de pesquisa binária e descobrimos a torre defeituosa em $O(\log(N))$. Para mais informações sobre este método confiram o artigo do loop:

Solução Ótima

Chegamos então aos últimos patamares, que são definitivamente os mais difíceis. Até agora conseguimos escapar-nos ao problema em si aproveitando propriedades de árvores ou de grafos em linha, mas agora já não temos mais como fugir.

A primeira ideia que surge naturalmente depois de passarmos pela solução anterior de pesquisa binária: e se conseguíssemos fazer pesquisa binária numa árvore? O problema parece sugerir que conseguimos!

Todas as árvores contêm o que se chama de um centroide, que é um nó que se for removido particiona a árvore em várias componentes com no máximo $N / 2$ nós cada uma. Por outras palavras, se colocarmos esse nó como a raiz da árvore, todas as suas subárvores têm no máximo $N / 2$ nós cada uma. Para quem não conhece os conceitos de raiz, subárvore, etc, a imagem seguinte explica-os visualmente.

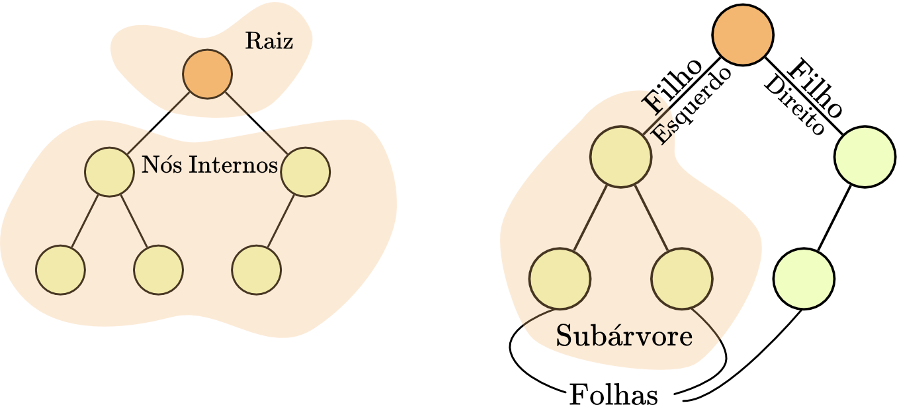
É possível provar que o centroide existe sempre se repararmos que escolhendo um nó qualquer de uma árvore, se este não for um centroide, então tem exatamente uma subárvore com mais de $N / 2$ nós. Se escolhermos o seu vizinho mais próximo dessa subárvore, a maior subárvore do novo nó tem de ser menor que a maior subárvore do nó anterior. Logo eventualmente teremos de chegar a um centroide. Voltaremos a esta prova com mais detalhe num outro artigo do loop.

O novo algoritmo agora passa por começar por adivinhar o centroide da árvore original. Quando nós indicam o vizinho mais próximo do nó que adivinhámos, passamos a saber que o nó defeituoso se encontra na subárvore do nó indicado. Logo, temos agora apenas $N / 2$ nós a considerar. Se agora adivinharmos o centroide da nova árvore com apenas $N / 2$ nós e o fizermos sucessivamente até encontrarmos o nó defeituoso, vamos precisar de no máximo $O(\log(N))$ iterações, analogamente ao que acontecia com a pesquisa binária numa lista.

Assim, agora a diferença entre ter 75 pontos ou ter 100 pontos está em como calculamos o centroide de cada árvore para aplicar o algoritmo anterior: um método $O(N^2)$ dar-nos-ia 75 pontos e um método $O(N)$ 100 pontos.

Para calcular o centroide de uma árvore em $O(N)$ começamos por escolher um nó qualquer como a raiz da árvore. De seguida, calculamos o tamanho de cada subárvore "descendente" de cada nó. Por subárvore descendente queremos dizer todas as subárvores que se afastam da raiz, ou seja, não consideramos a subárvore do nó dado que contém a raiz. Para calcularmos este tamanho, basta fazermos uma pesquisa em profundidade na árvore e guardarmos o tamanho de cada nó no processo (como faríamos numa solução baseada em programação dinâmica). Se $S_i$ for o tamanho da subárvore que começa no nó $i$, então: $S_i = \sum_{c \in C_i}{S_c}$, onde $C_i$ são os filhos do nó $i$.

Agora podemos usar os valores de $S_i$ para iterar por todos os nós, olhar para os filhos de cada nó e determinar o máximo de todos os $S_c$, com $c \in C_i$, e $N - S_i$ (que corresponde ao tamanho da subárvore que contém a raiz, ou seja, todos os nós exceto os que estão em subárvores descendentes). Com isto podemos determinar o nó centroide linearmente e aplicar o resto do algoritmo.