Problema B - Passeio de metro

O Problema

Dado um conjunto de $N$ estações, a zona e o prémio associado a cada uma, assim como um custo de transporte $A$ e $B$ entre zonas e uma estação inicial $I$, calcular a melhor pontuação possível de obter num passeio segundo as condições do jogo

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

1 ≤ $N$ ≤ 100 000	Número de estações
1 ≤ $N_i$ ≤ 1 000 000	Prémio de cada estação
1 ≤ $Z$ ≤ $N$	Número de zonas
1 ≤ $A, B$ ≤ 1 000 000	Custo entre zonas
1 ≤ $I$ ≤ $N$	Estação inicial

Os casos de teste deste problema estão organizados em 6 grupos com restrições adicionais diferentes:

Grupo	Número de Pontos	Restrições adicionais
1	15	$I$ = 1; $N \leq$ 10; $A, B \leq$ 1 000
2	15	$I$ = 1; $N \leq$ 2 000
3	15	$N \leq$ 2 000
4	15	$I$ = 1; $Z \leq$ 2 000
5	20	$I$ = 1
6	20	-

Solução Base

Neste problema pedem-nos para escolher a melhor maneira de navegar entre um conjunto de estações, partindo de uma posição inicial $I$.

Como não vale a pena visitar a mesma estação duas vezes, o número máximo de caminhos válidos interessantes é igual ao número de maneiras de visitar um qualquer número de estações. Este valor está relacionado com o fatorial do número de estações, $N!$, visto que temos cerca de $N$ maneiras de escolher a primeira estação a visitar, $N - 1$ para escolher a segunda e por ai fora.

Assim, a solução mais simples possível passa por experimentar cada um destes $N!$ caminhos possíveis, calcular o prémio para cada um deles e imprimir o melhor que encontrarmos. Podemos implementar uma solução recursiva que considera um estado como um conjunto de estações visitadas mais a última estação que visitámos e que vai visitando novas estações e calculando o seu custo.

Nota que esta solução funciona independentemente do $I$ escolhido (se for bem implementada), mas só conseguirá bater o primeiro grupo de casos de teste. Se por alguma razão não conseguissem ter esta solução a funcionar para qualquer $I$, podiam ter na mesma os 15 pontos deste grupo.

Esta seria uma solução $O(N!)$ que daria aproximadamente 15 pontos.

Alternativa para melhorar

Uma curiosidade que permite melhorar esta solução e fazer com que ela funcione até $N = 20$ (o que infelizmente não daria mais pontos na prova), seria pensar em como otimizar a nossa representação de estados. Podemos combinar isso com uma técnica clássica de programação dinâmica chamada programação dinâmica com bitmasks.

Não iremos entrar em muito detalhe aqui, visto que a solução é semelhante à solução clássica de exemplo desta técnica para o problema do traveling salesman. Fica o artigo do loop que cobre esta técnica (entre outras) e que requer que já conheçam os básicos de programação dinâmica.

Solução Melhorada

Vamos agora raciocinar em como melhorar a solução anterior. Para simplificar, vamos primeiro pensar apenas na solução para $I$ = 1 e depois veremos como usar esta solução para o caso mais geral.

Com I = 1

Se começamos na primeira estação, começamos por observar que nunca temos de voltar para trás, basta-nos andar sempre para uma estação a seguir. A razão para isto é a seguinte: imaginemos que a solução ótima parte da estação $a$, viaja para a estação $c$ e depois para a estação $b$, onde $a < b < c$. Neste caso, basta modificarmos a solução para viajar de $a$ para $b$ e posteriormente para $c$ para obtermos uma solução tão boa ou melhor que a anterior, por isso nunca é ótimo voltar para trás.

Com isto em mente, podemos pensar em como calcular a melhor pontuação considerando todas as estações até a uma dada estação $x$ e usar estes resultados para calcular a melhor pontuação para a estação $x$. Para evitar calcular múltiplas vezes o mesmo, podemos guardar estes valores, usando a técnica conhecida como programação dinâmica. Confiram o artigo do loop sobre o assunto:

Vamos denotar por $S_x$ a melhor pontuação possível de obter se terminarmos a nossa viagem em $x$. Para calcular $S_x$, vamos assumir que já calculámos $S_i$ para todos os $i < X$. Ora, como vamos terminar a nossa viagem em $x$, sabemos que a última viagem que vamos fazer termina em $x$. Assim, só temos de escolher qual foi a última estação a ser visitada. Se antes de chegar a $x$, a última estação foi $j$, então a pontuação da viagem final seria $S_j + C_{jx}$, onde $C_{jx}$ é o custo da viagem entre $j$ e $x$ (que pode ser calculado como: $A + B(Z_x - Z_j)$, onde $Z_i$ representa a zona da $i$-ésima estação). Se experimentarmos todas as estações $j$ possíveis e calcularmos a pontuação obtida se as considerássemos como última estação, $S_x$ será a melhor pontuação obtida.

Se guardarmos os valores de $S_x$ numa array sempre que calcularmos um e se calcularmos estes valores de 1 a $N$, a solução final será o maior $S_x$ calculado. Visto que apenas calculamos cada $S_x$ uma vez e que cada um necessita de iterar por no máximo $N$ estações, a complexidade temporal desta solução é $O(N^2)$.

Esta seria uma solução $O(N^2)$ que daria aproximadamente 30 pontos.

Para qualquer I

Agora que já sabemos como abordar o caso em que $I$ = 1, vamos estender a solução anterior para qualquer $I$.

Vimos que se $I$ for 1, então a viagem será linear, ou seja, nunca voltamos para trás. Se tivermos um $I$ qualquer, observamos uma propriedade semelhante, das duas uma: ou vamos de $I$ sempre para a direita e depois (potencialmente) sempre para a esquerda (passando $I$), ou vamos de $I$ sempre para a esquerda e depois (potencialmente) sempre para a direita (passando $I$). Nota que o "potencialmente" significa que podemos nunca virar para o lado contrário, ou seja, apenas considerar a mesma solução para $I$ = 1, mas para a esquerda e direita do $I$ a considerar. As imagens seguintes ilustram as duas situações:

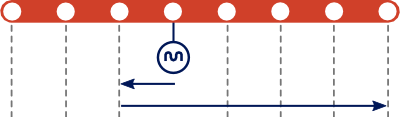
O raciocínio por detrás deste argumento é semelhante ao anterior, se tivermos uma solução que tenha mais que um "voltar atrás" podemos transformá-la numa solução com apenas um "voltar atrás" diminuindo ou mantendo o custo. Este argumento geométrico é fácil de se observar se esquecermos a situação atual de estações e viagens e pensarmos apenas que temos 3 pontos $a$, $b$ e $c$ em linha no plano, tal que $a$ está à esquerda de $b$ e $b$ à esquerda de $c$. Se pegarmos num lápis partindo do ponto $b$, qual é o caminho mais curto que podemos ter de modo a unir os três pontos com linhas sem nunca levantar o lápis?

Feita esta observação, como podemos usá-la a nosso favor? Ora, vamos primeiro dividir o problema em dois mais simples. Dividimos a linha de estações em duas, uma para a esquerda de $I$ e outra para a direita. Ficamos com duas linhas onde $I$ é a primeira estação. Agora aplicamos a nossa solução para $I$ = 1 em cada uma. Vamos imaginar que a solução é da forma descrita na situação 1 acima e considerar apenas este caso (o segundo caso é análogo). Para cada valor de $S_x$ para a linha à direita de $I$ podemos voltar para trás e depois percorrer a melhor solução possível para a linha à esquerda. Assim, temos no máximo $2N$ caminhos a testar: dois para cada estação à direita de $I$. Dada uma estação $x$ à direita de $I$, consideramos o caminho que termina em $x$ (que tem pontuação $S_x$) e o caminho que vai de $I$ a $x$ e depois de $x$ à posição $d$ à esquerda de $I$ à qual corresponde o melhor $S_d$ (que tem pontuação $S_x - C_{xI} + S_d$).

A complexidade temporal desta solução é $O(N)$ mais a complexidade da solução para $I$ = 1, que é aplicada duas vezes, ou seja, no total é $O(N^2)$. Nota que basta-nos melhorar a solução para $I$ = 1 para melhorarmos esta solução, facto que iremos aproveitar nas próximas soluções.

Esta seria uma solução $O(N^2)$ que daria aproximadamente 45 pontos.

Solução Intermédia

Um dos grupos de casos de teste tem um limite para o número de zonas, o que nos indica que é possível melhorar a nossa solução anterior fazendo algumas observações para as zonas.

Visto que entre duas estações dentro da mesma zona, o custo de viagem é sempre $A + B$, podemos pre-calcular as estações dentro de uma zona que vale a pena visitar: serão todas as que tenham prémio superior a $A + B$. Se calcularmos este valor para cada zona em $O(N)$, podemos comprimir a lista de estações a uma lista de zonas em que o prémio de uma zona é igual à pontuação obtida ao visitar todas as estações que vale a pena visitar nessa zona. Assim, agora podemos aplicar a nossa solução anterior mas numa linha de zonas em vez de numa linha de estações! A única mudança a fazer é que agora a função de custo dadas duas zonas $i$, $j$ é $C_{ij} = A + B(j - i)$, pois $i$ e $j$ representam a própria zona.

Isto melhora a complexidade de aplicar a solução para $O(Z^2)$, pois agora a linha de zonas tem apenas $Z$ zonas.

Esta seria uma solução $O(Z^2 + N)$ que daria aproximadamente 80 pontos.

Solução Ótima

O último passo a fazer para obter a solução ótima deve ser mais óbvio agora que vimos a solução intermédia. Se pensarmos no resultado de comprimir as estações em zonas, ficaremos com algumas zonas que nunca vale a pena visitar (as que não têm nenhuma estação que vale a pena visitar) e todas as restantes valerá sempre a pena visitar. Assim, podemos aplicar uma solução greedy para o caso $I$ = 1 que escolhe como próxima zona sempre a próxima zona que vale a pena visitar, evitando assim percorrer todas as zonas anteriores para calcular a $S_x$ para uma zona $x$.

Para tal, apenas precisamos de iterar por todas as zonas e atualizar a pontuação sempre que chegamos a uma zona que vale a pena visitar. Isto, naturalmente, pode ser feito em $O(Z)$.

Nota que não precisávamos necessariamente da compressão de zonas para aplicar esta solução, podemos estender o mesmo raciocínio a estações e obter uma solução que caminha sempre para a próxima estação que vale a pena visitar.

Esta seria uma solução $O(N)$ que daria exatamente 100 pontos.

Problema Alternativo

Podemos fazer uma pequena modificação ao problema e obter um problema bastante mais difícil (e interessante). A nossa função de custo entre duas zonas é linear, ou seja, $C_{ij} = A + B(i - j)$ é uma função linear. Se em vez desta função linear, tivéssemos uma qualquer função crescente, ou seja, uma função onde percorrer $k_1$ zonas é sempre mais custoso do que percorrer $k_2$ zonas se $k_1 > k_2$, mas que os valores entre zonas podem variar (sendo dados como input do problema), o que alterava nas nossas soluções?

Para este problema, todas as soluções que descrevemos são válidas com exceção da última (a ótima), pois já não podemos aplicar o mesmo passo greedy. A razão para tal é que podemos ter que visitar uma zona que não vale a pena visitar (segundo a descrição da solução) para diminuir o custo de viagem. Por exemplo, se viajar entre 2 zonas tiver custo 4, mas viajar entre 4 zonas tiver custo 1000, pode valer a pena em vez de atravessar 4 zonas entre duas zonas que valem a pena serem visitadas, fazer uma paragem intermédia numa zona entre elas para evitar o alto custo entre 4 zonas.

Neste caso a única possibilidade que temos para obter uma solução melhor que a quadrática é melhorar a maneira como calculamos os valores de $S_x$ na nossa solução de programação dinâmica. Consegues ver como fazê-lo? Dica: é útil escrever a fórmula de $S_x$ como uma função de otimização (um máximo entre alguns valores) e depois ver como podemos evitar ter que passar por todos esses valores para determinar o maior, utilizando, por exemplo, uma estrutura de dados eficiente.