Problema A - Chegar ao outro lado

O Problema

Dado $N$, o número de pontos da rua e o tempo que demora percorrer o cada segmento entre cada par, $S$ o número de passadeiras (com semáforo), $S$ inteiros que representam o tempo de atravessar cada passadeira e $Q$ perguntas indicando dois pontos, para cada pergunta imprimir a distância mínima entre os dois pontos dados.

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

1 ≤ $N$ ≤ 100 000	Tamanho da rua do Simão
1 ≤ $S$ ≤ $N$	Número de passadeiras
0 ≤ $P_i$ ≤ $N$ - 1	Posição das passadeiras
1 ≤ $T_i$, $N_i$ ≤ 1 000 000	Tempo associado aos semáforos e entre segmentos
1 ≤ $Q$ ≤ 100 000	Número de perguntas
0 ≤ $A_i$, $C_i$ ≤ $N$ - 1	Posição dos pontos das perguntas
1 ≤ $B_i$, $D_i$ ≤ 2	Número do passeio dos pontos das perguntas

Os casos de teste deste problema estão organizados em 6 grupos com restrições adicionais diferentes:

Grupo	Número de Pontos	Restrições adicionais
1	15	$N$ ≤ 20, $S$ = 1
2	15	$S$ = 1
3	15	$N$, $S$, $Q$ ≤ 1 000
4	15	$A_i$ = $C_i$
5	20	$N$, $S$, $Q$ ≤ 30 000
6	20	-

Solução para o grupo 1

Neste grupo de testes temos um valor de $N$ pequeno e apenas uma passadeira. Na solução para cada pedido, apenas existe um caminho entre dois pontos que não repete nenhum ponto, logo apenas temos que calcular o tamanho desse caminho que, obviamente, é melhor que qualquer solução que repita pontos.

Assim, temos dois casos, ou os pontos de um pedido estão no mesmo passeio, ou estão em passeios diferentes. No primeiro caso podemos simplesmente fazer um ciclo que simule o caminho a percorrer dum ponto ao outro. No segundo fazemos algo semelhante, mas agora queremos a distância de cada ponto à passadeira, e no fim adicionamos o tempo de atravessar a passadeira.

Esta solução é $O(NQ)$ e assume que $S$ = 1, e assim daria apenas os primeiros 15 pontos.

Solução para o grupo 2

Este grupo de testes é semelhante ao anterior, mas $N$ e $Q$ têm valores muito superiores. Assim, precisamos de algo que nos permita calcular as distâncias necessárias de maneira mais eficiente. Para isso, vamos pre-calcular a distâncias entre certos pontos, usando uma técnica conhecida como somas acumuladas. Esta técnica é baseada em programação dinâmica, que consiste explorar a estrutura de um problema de forma a não calcular valores que já tenham sido calculados. Para lerem mais sobre ambas podem consultar o seguinte artigo do loop:

As distâncias tem uma propriedade que podemos aproveitar: Se tivermos três pontos $A$, $B$, $C$ na mesma linha, em que $A < B < C$, a distância entre $A$ e $C$ é igual à distância entre $A$ e $B$ mais a distância entre a $B$ e $C$. Além disso, a distância entre $B$ e $C$ é igual à distância entre $A$ e $C$ menos a distância entre $A$ e $B$. Assim, se guardarmos as distâncias entre o ponto 0 e qualquer outro ponto em ambas as linhas podemos calcular a distância entre dois pontos em $O(1)$! É apenas a distância entre 0 e o ponto mais à direita menos a distância entre 0 e o mais à esquerda. Assim, modificamos a solução anterior para calcular a distâncias entre os pontos de interesse em $O(1)$ (o que corresponde à ideia das somas acumuladas).

A solução fica, assim, com complexidade temporal de $O(N)$ e assume que $S$ = 1, ficando assim com 30 pontos.

Solução para o grupo 3

Neste grupo podemos assumir que $N$, $S$ e $Q$ não ultrapassam 1000. Assim, uma solução de pesquisa exaustiva para descobrir cada distância é suficiente para respeitar os limites temporais.

Se conseguirmos calcular a distância entre dois pontos em $O(N)$ temos uma solução que responde cada pedido em $O(N)$ e que resulta numa complexidade temporal total de $O(NQ)$. Primeiro andamos para trás para calcular a menor distância entre os pontos de diferentes passeios na primeira coordenada. Para fazer isso temos um ciclo que parte da coordenada e vai somando os valores de cima e baixo, e sempre que encontra uma passadeira verificamos se é melhor do que temos atualmente. Depois partimos com dois valores: o melhor andando em cima e o melhor andando em baixo, sendo que o passeio do ponto que partimos começa com valor 0 e o outro com distância que encontramos (ou um valor a sinalizar caso não haja passadeiras atrás).

De seguida vamos percorrendo o caminho somando os valores de cada passeio ao caminho correspondente e sempre que encontramos uma passadeira atualizamos os valores de cada um dos lados considerando vir pelo outro lado adicionar o valor da passadeira. Ou seja, verificamos para cada um se o valor de vir do outro mais a passadeira é menor que o valor atual desse. Finalmente, ao chegar à coordenada final repetimos o processo inicial e o valor pretendido é o melhor entre o valor do passeio onde queremos estar e o valor do outro passeio mais o que calculámos.

Assim, obtemos uma complexidade temporal de $O(NQ)$ obtendo 30 pontos (15 deste grupo mais 15 do primeiro).

Solução para o grupo 4

Agora podemos assumir que os pontos das perguntas partilham coordenadas. Para isto usaremos algumas observações que facilitam a análise.

Primeiro, verificamos que o caminho mais curto encontra-se totalmente à esquerda ou totalmente à direita da dupla de pontos do pedido, ou seja, não passa por pontos do lado esquerdo se passa por algum do lado direito e vice versa. Isto pois para mudar de lado implica repetir pelo menos o ponto inicial, tornando inútil o caminho de um dos lados.

Assim, é possível de observar que apenas passamos por um passadeira. Ao utilizar 2 ou mais vamos sempre repetir algum ponto. Logo, apenas temos de testar a distância andando sempre para a direita e depois voltar (atravessando uma passadeira), e sempre para a esquerda e voltar usando apenas uma passadeira. A imagem seguinte ilustra os dois casos (um a vermelho e outro a verde):

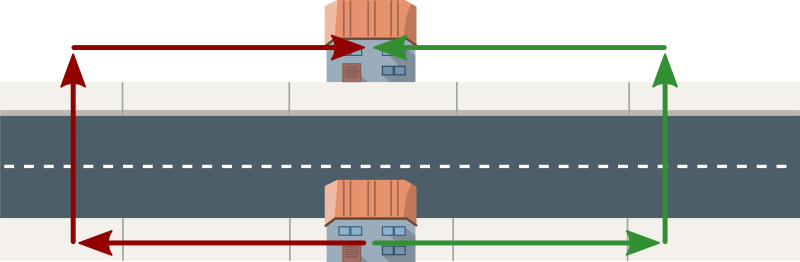
Com isto vamos calcular para cada ponto a melhor distância de um passeio para o outro e guardar, para depois para cada pedido bastar simplesmente ir buscar o valor já calculado.

Resolvemos os dois casos em separados e posteriormente escolhemos o melhor dos dois. Visto que a solução para dos dois sentidos é análoga, veremos apenas o caso em que a solução está totalmente à esquerda da dupla de pontos.

Primeiro, todos os pontos que não têm uma passadeira em qualquer ponto à sua esquerda são desconsiderados (a resposta terá obrigatoriamente de passar pela direita). De seguida, aos pontos ligados pela primeira passadeira da esquerda atribuímos o tempo associado a atravessar essa passadeira. Para cada ponto seguinte à direita, a menor distância para o atingir será o menor entre:

• a menor distância do ponto anterior (à esquerda) mais o tempo entre pontos adjacentes de cima e baixo;
• caso haja uma passadeira, o tempo de passar essa passadeira;

Cada um destes valores corresponde à melhor forma de chegar de um ponto ao ponto oposto (no passeio oposto). Como apenas precisamos de um ciclo, podemos calcular estes valores com complexidade temporal $O(N)$ e responder a cada pedido em $O(1)$. Nota: neste grupo podemos ter casos em que o ponto de partida e destino são os mesmos, estes casos têm de ser tratados à parte (a resposta é trivial).

Assim recebemos os 15 pontos correspondentes a este grupo. No total já obtemos 60.

Solução para o grupo 5

Temos agora que $N$, $Q$ e $S$ são sempre menores que 30 000. Logo, teremos de ter uma solução geral mais eficiente que a anterior de calcular a distância entre dois pontos em $O(N)$.

Para isto, vamos escolher $k$ pontos igualmente espaçados (já indicaremos como escolher o valor de $k$) em cada um dos passeios (para cada ponto escolhemos também o seu oposto, no outro passeio). Para cada um destes pontos, calculamos a distância a todos os outros com a solução do grupo 3. Depois, para cada pedido podem acontecer duas coisas:

• Existe um ponto dos que selecionamos no meio dos dois pontos do pedido. Neste caso, visto que qualquer caminho entre os dois pontos do pedido terá de passar neste ponto (ou no do passeio de cima, ou no do passeio de baixo), a melhor solução terá de passar por este ponto. Como calculámos anteriormente a melhor forma de chegar a todos os pontos a partir de qualquer ponto selecionado, a resposta será o caminho mais curto entre o primeiro ponto do pedido e um dos pontos opostos selecionados, mais o caminho mais curto entre o mesmo ponto selecionado e o segundo ponto do pedido.

• Não existe nenhum ponto selecionado entre os pontos do pedido. Neste caso, a resposta terá que: ou passar por menos que $N / k$ pontos (pois existe um ponto selecionado a cada $N / k$ pontos); ou passar por um dos quatro pontos selecionados à volta dos dois do pedido (os dois mais próximos de cada lado). Para a primeira situação, podemos usar a solução do grupo 3, mas parar quando explorarmos mais que $k$ pontos. Na segunda, podemos fazer o que já tínhamos feito no primeiro caso, de usar cada ponto selecionado como intermédio.

Assim, a complexidade temporal final é $O(Nk + Q(N / k))$. Queremos escolher um $k$ que minimize esta expressão e é possível calcular (e intuitivamente faz sentido) que esse valor é $\sqrt(N)$, resultando na complexidade de $O(N\sqrt(N) + Q\sqrt(N))$, obtendo os 20 pontos do grupo de casos de teste (também resolve os grupos 1 e 3 e, compondo com as soluções anteriores, podemos chegar a 80 pontos).

Solução para o grupo 6

Chegamos ao último grupo, que corresponde à solução mais ótima.

Antes de mais, observemos a seguinte imagem:

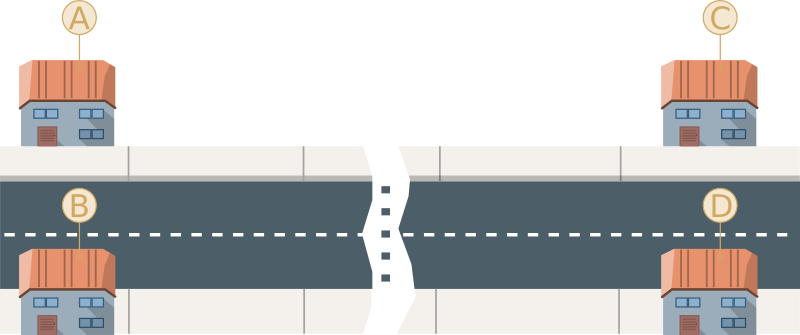
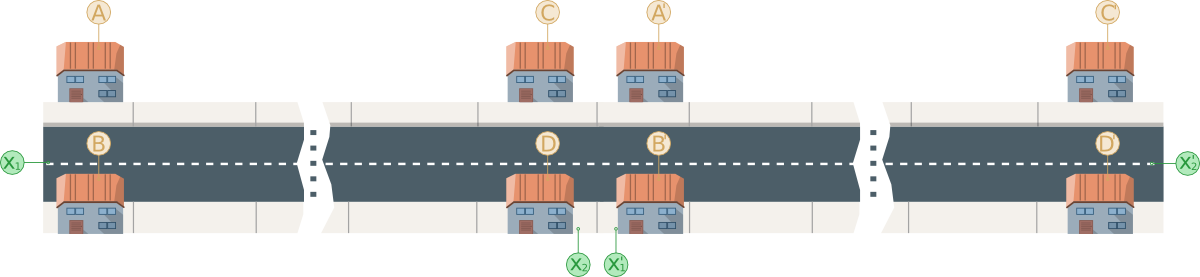
Denotaremos às distâncias entre dois pontos $A$ e $B$ por $\overline{AB}$. Quando $A$ = $C$ e $B$ = $D$ é fácil determinar as distâncias entre eles: $\overline{AC}$ = $\overline{BD}$ = 0 e $\overline{AD}$ = $\overline{BC}$ = distância mínima entre os pontos (calculada na grupo 4). Agora imaginemos que temos as mesmas distâncias para dois intervalos adjacentes como na figura seguinte (carreguem na imagem para a aumentar):

Utilizando o que já sabemos para os dois intervalos ($x_1$ a $x_2$ e $x_1'$ a $x_2'$) podemos juntar e calcular para o intervalo maior ($x_1$ a $x_2'$). O cálculo de cada um é semelhante, apenas temos de considerar dois casos: o em que o segmento de $C$ para $A'$ pertence ao caminho mais curto; e a que o segmento de $B$ para $D'$ pertence ao caminho mais curto. Por exemplo, a distância entre $\overline{AC'}$ é igual ao mínimo entre $\overline{AC} + \overline{A'C'} + \overline{CA'}$ e $\overline{AD} + \overline{B'C} + \overline{DB'}$.

Com isto podemos construir uma estrutura como uma árvore de segmentos que guarda estes 4 valores para certos intervalos e permite a distância para qualquer intervalo em $O(\log(N))$. Para um dado pedido apenas temos de considerar três casos (como em qualquer árvore de segmentos):

• o intervalo atual pertence totalmente ao pedido e devolvemos o seu valor;
• o intervalo atual não pertence ao pedido e por isso não é relevante para a solução;
• o intervalo atual pertence parcialmente, nesse caso fazemos dividimos o pedido em dois intervalos e calculamos o resultado do pedido para cada um, juntando como foi explicado nos primeiros parágrafos;

No fim é só imprimir o valor associado à situação pedida no pedido. Para saberem mais sobre árvores de segmentos, fica o artigo do loop sobre o assunto:

Esta solução resolve todos os grupos e obtém, merecidamente, os 100 pontos.