6. Estruturas de dados
O próximo tema está relacionado com dados e a sua representação. Já vimos problemas com diferentes tipos de dados a processar: sequências de números, textos, pontos, etc. Para estes problemas foi importante representar o input de alguma forma no nosso programa e usámos simples arrays para tal. Como iremos ver, a representação de um objeto num programa é mais do que guardar objetos no nosso programa, tem influência na eficiência de extrair informação dos nossos dados.
Memória e apontadores
Visto que vamos falar de representação de dados num programa, é uma boa altura para falarmos um pouco sobre como é que funciona a memória de um computador e como podemos usar essa informação para nossa vantagem. É importante notar que vamos apenas ver um modelo simplificado de memória, o funcionamento real da memória de um computador é bastante mais complexa. Porém, para o nosso propósito o modelo simplificado é mais que suficiente. Posteriormente, vamos falar de apontadores, um tópico que possivelmente já ouviram falar quando aprenderam a programam, mas que vamos voltar a ver.
Um modelo simples de memória
Vamos imaginar o nosso modelo de memória como uma fita de pequenos interruptores. Cada interruptor tem dois estados: "ligado" ou "desligado". Um estado binário como este é conhecido como um bit. Medimos a capacidade de representação da nossa memória como número de bits que a sua fita contém. Para simplificar a notação, usamos algumas unidades intermédias: um byte são 8 bits; um kilobyte são 1000 bytes; um megabyte são 1000 kilobytes; um gigabyte são 1000 megabytes. É importante saber esta notação porque a memória que o nosso programa tem disponível é limitada, regra geral as submissões no Mooshak são limitadas a 256 megabytes.

Quando queremos representar algum tipo de dados, temos de reservar
parte desta fita (ou seja, alguns dos seus interruptores) a
representar o que queremos. Por exemplo, se quisermos guardar um
inteiro e usarmos uma variável do tipo int, precisamos de 32 bits
ou 4 bytes, por isso precisamos de 32 interruptores a guardar o
estado exato da nossa variável.
A enorme fita de interruptores que um computador tem disponível é partilhada por todos os programas que estão a correr ao mesmo tempo. Assim, sempre que precisamos de uma nova array precisamos de reservar algum espaço na fita. Chamamos a este processo de "alocar memória". Notem ainda que esta reserva de espaço tem de ser dinâmica pois não sabemos quanto é que cada programa vai usar, o que torna este processo bastante complicado. Felizmente, o compilador e o sistema operativo do computador fazem este trabalho por nós.
Um último conceito que pode ser interessante sabermos é a distinção
entre memória estática e dinâmica. Estes tipos de memória são apenas
divisões que impomos na nossa fita para representar tipos de dados
diferentes. Para correr um programa, o computador (mais
especificamente, o sistema operativo, que é quem lida com a execução
de programas) tem de guardar várias coisas sobre o programa a executar
e o ambiente de execução. Algo tão simples como "que linha do programa
tenho de executar a seguir?" tem de ser guardado algures e este tipo
de informação é guardada numa zona de memória estática. Já a memória
dinâmica está normalmente dividida em dois tipos a memória do tipo
stack e a do tipo heap. A memória do tipo stack está normalmente
associada a variáveis locais (por exemplo, uma variável do tipo int
é normalmente local) e a outros dados auxiliares (por exemplo, dados
auxiliares que o sistema operativo mantém quando uma função é chamada
para saber para onde devolver o resultado). A memória do tipo heap é
global. Quando alocamos memória estamos a alocar parte da memória
heap. Uma distinção importante da memória stack para a heap é
que a algo guardado em memória stack é libertado automaticamente
quando saimos do âmbito onde foi declarado, o mesmo já não se verifica
para algo em memória heap. Porque é que isto é um problema? O
computador (sistema operativo) não sabe que já não vamos usar uma
certa array e por isso vai mantê-la em memória até a libertarmos ou
o programa terminar. Veremos exemplos disto mais à
frente. Adicionalmente, é importante dizer que isto apenas se aplica a
C++ e Pascal, linguagens como Java usam um mecanismo chamado de
garbage collection que deteta objetos em memória heap que já não
são usados e liberta-os. Vamos ver um exemplo dos vários tipos de
memória em ação:
int arr1[100];
int main() {
int arr2[100];
int* arr3 = new int[100];
return 0;
}Neste programa, a arr1 ficará guardada em memória estática, a arr2
em memória dinâmica do tipo stack e a arr3 em memória dinâmica do
tipo heap. Possivelmente nunca viram algo do tipo int*, um objeto
deste tipo é um apontador para um inteiro. Na próxima secção abordamos
este assunto.
Para terminar esta secção, uma breve nota sobre o quão próximo da realidade é este modelo de memória. Um computador usa uma hierarquia de memórias físicas de diferentes tipos, umas mais rápidas mas com menos capacidade de armazenamento, outras mais lentas mas com mais capacidade de armazenamento, para criar esta "ilusão" de uma memória em fita. Não iremos abordar o seu funcionamento, pois não é muito relevante para o tipo de problemas que são propostos nas Olimpíadas.
Apontadores
Seguindo a analogia da secção anterior, um apontador é uma referência para uma posição na fita de memória. Um apontador tem sempre um tipo associado, que indica o tipo representado na posição de memória para o qual aponta. Assim, um apontador é apenas uma variável que representa um índice da fita de memória. Vamos ver um exemplo de uso de apontadores em C++ (nota: aconselhamos a correrem cada um dos programas desta secção para estudarem o resultado):
#include <iostream>
using namespace std;
int main() {
int v1 = 5;
int* p1 = &v1;
v1 = 6;
cout << *p1 << endl;
*p1 = 4;
cout << v1 << endl;
return 0;
}Vamos descontruir o programa anterior. A declaração int* p1 indica
que p1 é um apontador de inteiros. Para lidar com apontadores em C++
há dois operadores importantes: o operador & e o operador *. O
operador & devolve o índice de uma variável, ou seja, ao fazemos p1
= &v1 estamos a dizer que o apontador p1 aponta para a posição da
memória onde se encontra guardada a variável v1. Já o operador *
faz o reverso, devolve o valor da variável guardada na posição de um
apontador, ou seja, *p1 devolve o valor da posição de memória para a
qual p1 aponta.
Agora, qual será o resultado do programa anterior? Ao escrevermos
int* p1 = &v1 temos que o apontador p1 aponta para a posição de
memória onde se encontra v1. Ao mudarmos v1 para 6 e
posteriormente imprimirmos *p1, ou seja, o valor na posição de
memória para a qual p1 aponta, vamos imprimir exatamente 6. De
seguida, ao escrevermos *p1 = 4 estamos a mudar o valor da posição
de memória para a qual p1 aponta. Visto que esta posição é
exatamente a mesma onde está guardada a variável v1, de seguida ao
imprimirmos v1 vamos imprimir 4.
Vamos agora ver um uso ligeiramente diferente de apontadores, que ao início poderá parecer um pouco estranho:
#include <iostream>
using namespace std;
int p1[100];
int main() {
*p1 = 5;
cout << p1[0] << endl;
*(p1 + 5) = 2;
cout << p1[5] << endl;
return 0;
}Uma array em C++ não é mais que um apontador! Quando declaramos uma
array o que nos é devolvido é um apontador para a posição inicial de
um intervalo de memória é alocado para a nossa array. Assim, quando
fazemos *p1 = 5 no exemplo acima, estamos a mudar a primeira posição
da array para o valor 5. Adicionalmente, a array é alocada num
intervalo contíguo, o que significa que podemos obter o índice de
memória de qualquer posição com uma simples soma! Se nos lembrarmos
que um apontador refere uma posição na fita de memória, ao
somarmos-lhe um valor estamos a obter uma posição mais à frente, ou
seja, quando fazemos *(p1 + 5) = 2 estamos a mudar o valor da
posição 5 da array para 2, algo que podemos verificar ao imprimir o
valor correspondente usando a notação que conhecemos p1[5].
Isto significa ainda que uma array bidimensional é apenas um apontador para um apontador de um certo tipo. Para confirmarmos este novo facto, vamos ver uma forma de alocar arrays dinamicamente, e assim ter uma array do tamanho que quisermos.
#include <iostream>
using namespace std;
int main() {
int n;
cin >> n;
int* arr = new int[n];
arr[5] = 4;
cout << arr[5] << endl;
int** arrarr = new int*[2];
arrarr[0] = arr;
arrarr[1] = arr;
arrarr[0][3] = 2;
cout << arr[3] << endl;
delete arr;
delete arrarr;
return 0;
}Aqui estamos a alocar uma array dinamicamente usando o operador
new. A variável arr comporta-se como uma array normal, podemos
fazer o que quisermos, com a única diferença que foi alocada
dinamicamente. Como exemplo lúdico, temos ainda uma array de
arrays que declaramos como int** arrarr = new int*[2], ou seja, um
apontador para apontador de inteiro que é declarado ao alocar uma
array com dois elementos. Nas linhas seguintes colocamos cada um dos
elementos desta array de arrays igual a arr e de seguida podemos
ver como ao a usar como uma array bidimensional normal tem o efeito
desejado. Finalmente usamos o operador delete para libertar a
memória que alocámos, exatamente porque, como foi referio, a memória
dinâmica que é alocada tem de ser libertada manualmente e é usando o
operador delete que o podemos fazer.
Para terminar esta secção, lembramos que um apontador funciona como um
índice para uma posição de memória, por isso podemos fazer várias
operações comuns que faríamos a um inteiro. Existem outros exemplos
mais avançados do uso de apontadores, mas vamos ver uma simples (mas
não muito prática) forma de percorrer uma string/array de
char. Lembramos que uma string é sempre terminada pelo carácter
\0, mas deixamos a interpretação do exemplo como exercício.
#include <iostream>
using namespace std;
char str[100];
int main() {
cin >> str;
char* p = str;
while (*p != '\0') {
cout << *p << endl;
p++;
}
return 0;
}Agora é uma boa altura para rever algumas das referências de introdução à programação e voltar a estudar apontadores com mais detalhe, para garantir que percebem bem este tema importante.
Estruturas de dados
As secções anteriores foram um prelúdio para o tópico que realmente nos interessa neste artigo: estruturas de dados.
Uma estrutura de dados é uma forma de organizar ou guardar um conjunto de dados, com o objetivo de poder extrair informação de forma eficiente. Neste sentido, uma array é um tipo de estrutura de dados, que representa um conjunto de elementos de forma sequêncial e permite acesso ao $i$ésimo elemento eficientemente (em tempo constante). Vamos motivar esta definição com um exemplo, como sempre.
A mesa da sala do Diogo está ornamentada com uma linha de $N$ velas de diferentes alturas. Para decidir quais quer acender, o Diogo quer saber alguma informação sobre as velas, nomeadamente, para cada vela o Diogo quer saber qual é a vela mais próxima à sua esquerda na linha de velas que é mais baixa que a própria vela. Isto é, quer saber para cada vela, qual a primeira vela que a precede cuja altura é menor que a da própria vela.
Suponhamos que $N = 6$ e a altura das velas na linha é $[4, 1, 3, 3, 7, 3]$, então a primeira vela não tem velas mais baixas à sua esquerda, a segunda também não, já as terceira e quarta velas têm como vela mais baixa mais próxima à esquerda a segunda vela (de altura 1), a quinta vela é logo precedida pela quarta vela (de altura 3) e finalmente a última vela tem a segunda vela como mais próxima à esquerda e mais baixa (de altura 1).
Nos casos de teste maiores, $N$ poderá ser tão grande como $100.000$, o que significa que precisamos de uma solução que seja $O(N)$ ou $O(N \log N)$ para conseguir resolver este problema. Podemos pensar em usar algumas das ferramentas que vimos anteriormente, como ordenar e aplicar uma pesquisa binária, mas se pensarem um pouco verão que não é fácil aplicá-las aqui.
Comecemos por fazer algumas observações sobre o problema. Antes de mais, vamos considerar que a vela na posição 5 tem altura 4 e a vela na posição 10 tem altura 2. Não é difícil de observar que para todas as velas das posições 11 em diante é impossível que a sua vela mais baixa mais próxima seja a vela na posição 5, exatamente porque a vela na posição 10 vai estar sempre mais próxima e tem uma altura ainda menor! Com esta observação em mente vamos tentar calcular o pretendido da primeira para última vela, ou seja, calculamos primeiro a vela mais próxima e mais baixa da vela na posição 1, de seguida para a vela da posição 2 e por ai fora. Seguindo a observação anterior vamos manter uma lista de velas que são candidatas a serem uma vela mais próxima de uma das velas que ainda não processámos. Cada vela nesta lista é representada por um par de números: uma posição na linha e uma altura, que definem unicamente uma vela. Assim, sempre que processamos uma nova vela vamos atualizar esta lista, nomeadamente removendo todas as velas com altura maior do que a altura da vela que estamos a processar, exatamente porque, como vimos, nenhuma destas velas pode ser a mais próxima de uma vela futura.
Resumindo o anterior, o nosso algoritmo é então: mantemos uma lista de velas inicialmente vazia. Vamos processar a linha de velas da primeira para a última. Para processar cada vela, começamos por apagar todas as velas na lista de velas que têm altura superior à que estamos a processar. Das restantes, procuramos a que está mais próxima da vela que estamos a processar, que será a resposta para a vela que estamos a processar. Inserimos a vela que acabámos de processar na lista.
Apesar de não ser muito complicado, este algoritmo requer alguma abstração mental, por isso é recomendado que experimentem um exemplo manualmente (com o exemplo dado anteriormente), escrevendo as velas que mantêm na lista à parte e passando por cada vela na linha.
Qual é a complexidade temporal deste algoritmo? Bom, infelizmente o nosso algoritmo é ligeiramente incompleto, mencionamos que temos de manter uma lista de velas, mas não como é que a mantemos. Uma possibilidade é fazer o seguinte: mantemos duas arrays de tamanho $N$, uma onde cada posição tem ou não uma vela e a segunda que indica se uma certa posição tem uma vela ou não (se a posição 5 desta array for 1 a posição 5 da primeira array é uma vela, se for 0 então a posição 5 da primeira array está livre). Assim, para inserir elemento basta encontrar uma posição livre e preenchê-la e para remover basta marcar a posição como livre. Sendo assim, não é difícil de ver que inserir e remover têm uma complexidade temporal de $O(N)$, o que faz com que o algoritmo tenha uma complexidade temporal de $O(N^2)$. Mas isto não é suficiente para os limites que vimos inicialmente! Vamos ver como melhorar isto.
Para resolver este problema vamos imaginar que temos uma pilha onde podemos colocar números. Pensemos nisto como uma torre de legos, onde cada lego tem um número associado e podemos adicionar ou remover o lego do topo. Como exemplo, temos a imagem seguinte:
Esta será a nossa estrutura de dados, para já apenas abstrata, que iremos usar para resolver este problema. Vamos modificar o algoritmo anterior fazendo mais uma observação. Considerem o passo de encontrar a vela mais próxima, no nosso algoritmo anterior. Observem que a vela mais próxima é sempre a de maior altura na lista de velas. Porquê? Sempre que inserimos uma nova vela removemos todas as que têm altura maior, isto implica que se ordenarmos as velas por posiçao também estamos a ordenar por altura!
Como podemos usar isto para chegar a um algoritmo eficiente? Processamos a linha de velas da primeira para a última, como anteriormente. Vamos manter uma pilha com velas (o exemplo anterior mencionava apenas uma pilha de números, mas uma vela é apenas um par de números). Para cada vela, vamos removendo o a vela do topo da pilha enquanto a sua altura for maior ou igual do que a altura da vela a processar. Depois deste processo, a vela do topo da pilha é a resposta para a vela que estamos a processar. Terminamos por inserir a vela que acabámos de processar no topo da pilha.
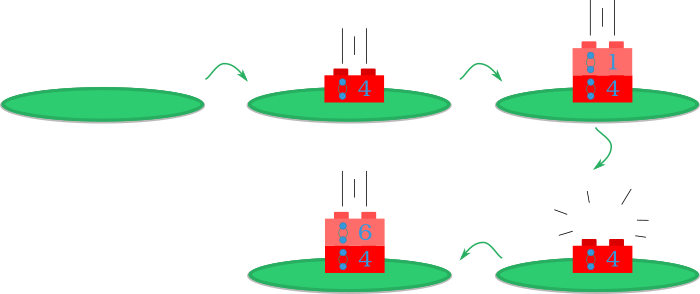
Ilustramos o comportamento da pilha neste algoritmo para o exemplo mencionado no início (a imagem apenas contém as alturas):

Qual a complexidade temporal deste algoritmo? Bom, parece que não melhorámos muito, visto que para cada vela podemos remover $O(N)$ velas da pilha, o que faria o nosso algoritmo novamente $O(N^2)$. Porém, reparem num pormenor importante: cada vela é inserida e removida exatamente uma vez da pilha, o que significa que a complexidade temporal total de inserir e remover elementos da pilha (ou seja, durante toda a execução do algoritmo) é de $O(N)$. Assim, a complexidade temporal deste algoritmo é de $O(N)$. Este argumento é ligeiramente subtil, pensem bem porque funciona. A ideia é que apesar de podermos ter que remover muitos elementos da pilha quando processamos uma das velas, para a maior parte das velas vamos remover muito poucos elementos (um número constante ou $O(1)$), em média vamos remover $O(1)$ elementos por vela e assim obtemos uma complexidade temporal total de $O(N)$.
Falta-nos apenas ver como realmente implementar esta estrutura de dados. Vamos ver duas implementações diferentes que são igualmente eficientes, nomeadamente que implementam cada operação em $O(1)$. Adicionalmente, vamos apenas mostrar a implementação para inteiros, é fácil de modificar a implementação para outros tipos de dados. Depois de saberem as duas implementações já têm todos os ingredientes para resolver este problema.

Problema I: Velas do Diogo
Este problema está disponível no Mooshak de treino como o problema I
Implementação 1
Vamos supor que sabemos o tamanho máximo da nossa pilha (no caso do algoritmo anterior, é obviamente $N$). A nossa implementação vai usar uma simples array e um contador, o qual vamos chamar da "cabeça" da pilha. O contador indica-nos quantos elementos há na pilha no momento da execução. Assim, conseguimos inserir um novo elemento ao colocá-lo na posição indexada pela cabeça e incrementando a cabeça, e remover um elemento ao decrementar a cabeça. A implementação desta ideia é bastante simples:
int seq[N]; // array base
int cabeca = 0;
void inserir_topo(int valor) {
seq[cabeca] = valor;
cabeca++;
}
void remover_topo() {
cabeca--;
}
int ver_topo() {
return seq[cabeca - 1];
}Implementação 2
Vamos agora remover a suposição anterior e vamos finalmente usar os apontadores que vimos anteriormente. Esta segunda implementação utiliza um conceito de "nó" que será um objeto que conterá um valor e um apontador para um outro nó. Para tal definimos uma struct recursiva usando apontadores:
struct no {
int valor;
no* proximo;
};Esta estrutura é recursiva no sentido em que contem um apontador para um objeto do mesmo tipo, a ideia é que vamos usá-la para encadear os elementos da pilha. Vamos supor que temos um nó especial que representa o topo da pilha, ao qual vamos chamar de cabeça. Para inserir um elemento na pilha criamos um novo nó com o valor pretendido, colocamos o seu próximo nó a apontar para a cabeça atual e marcamo-lo como a nova cabeça da pilha. Para remover basta marcar a cabeça da lista como o próximo nó da cabeça atual. Vejamos a implementação disto para perceber melhor (nota: usamos alguns conceitos de apontadores que explicamos de seguida):
no* cabeca = NULL;
void inserir_topo(int valor) {
no* novo_no = new no();
novo_no->valor = valor;
novo_no->proximo = cabeca;
cabeca = novo_no;
}
void remover_topo() {
no* cabeca_antiga = cabeca;
cabeca = cabeca->proximo;
delete cabeca_antiga;
}
int ver_topo() {
return cabeca->valor;
}Antes de mais, reparem que usamos o operador new de forma
ligeiramente diferente de anteriormente. Anteriormente usámos o new
para alocar dinamicamente uma array, mas desta vez usamo-lo para
criar um elemento do tipo no e colocar o apontador novo_no a
apontar para ele. Isto é semelhante ao que vimos no primeiro exemplo
de apontadores, onde em int* p1 = &v1 a variável p1 aponta para o
elemento representado pela variável v1. De seguida usamos um
operador novo, o operador ->. Este operador é usado com apontadores
de structs para aceder a um dos campos da struct que o apontador
referencia, ou seja, é exatamente igual a fazer (*novo_no).valor,
para o primeiro uso.
Este código faz exatamente o que mencionámos anteriormente, mas como quase tudo neste artigo, requer uma inspeção atenta para ser bem entendido.
Notas finais
Aqui acabámos por apenas mencionar uma estrutura de dados, nomeadamente uma pilha. Para resolver problemas algorítmicos de concursos é preciso uma mistura de saber usar e implementar estruturas de dados clássicas (como uma pilha) e inventar uma estrutura de dados que se adeqúe ao problema. No último artigo vamos mencionar alguns recursos para continuarem a aprender e a treinar para terem sucesso nas Olimpíadas, todos eles irão mencionar várias outras estruturas de dados que serão muito úteis, mas com o exemplo que vimos aqui já terão as bases para conseguirem entender e implementá-las.