5. Algoritmos e recursividade
Agora que já vimos o que significa analisar um algoritmo e como a solução de um problema implica mais do que simplesmente escrever um código que o resolve, vamos ver alguns exemplos de algoritmos/problemas clássicos e como podem ser aplicados em diferentes problemas. Adicionalmente, vamos visitar uma ideia que podem ainda não ter visto, nomeadamente a ideia de recursividade que consiste numa função que se chama a si própria (vamos ver como e porquê).
Ordenação
Ordenar um conjunto de números/palavras/elementos é um dos problemas mais fundamentais. A ideia é simples: é-nos dado uma sequência de números e queremos devolver a mesma sequência mas ordenada (por ordem crescente ou decrescente). Por exemplo, se a nossa sequência for $5, 2, 8, 3$ e a quisermos ordenar por ordem crescente o resultado é $2, 3, 5, 8$.
Como podemos fazer um programa que ordena uma sequência de números? Imaginemos que temos um baralho de cartas que precisamos de colocar em ordem, como podemos fazê-lo? Ora, uma possibilidade é fazer o seguinte (vamos ignorar a existência de naipes neste exemplo): encontramos o ás e colocamos no início, de seguida procuramos um 2 e colocamos a seguir ao ás, e por ai fora. De forma geral, este algoritmo o que faz é procurar a carta (número) de menor valor e coloca-lo no início. De seguida encontra o segundo maior, ou de forma equivalente o maior das restantes cartas (números), e coloca-lo na segunda posição. E por ai fora. Se quiséssemos implementar esta ideia em C++ poderiamos fazer o seguinte:
#include <iostream>
using namespace std;
int seq[100]; // Array para guardar a sequencia
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) // Ler a sequencia
cin >> seq[i];
for (int i = 0; i < n; i++) { // Encontrar o valor a colocar na posicao i
int mposicao = i; // Queremos o menor valor em seq de i a n
for (int j = i; j < n; j++)
if (seq[j] < seq[mposicao]) // Encontramos um menor que o que tinhamos
mposicao = j;
int temporario = seq[i]; // Trocar o valor na posicao i com o menor
seq[i] = seq[mposicao];
seq[mposicao] = temporario;
}
for (int i = 0; i < n; i++) // Imprimir a sequencia
cout << seq[i] << " ";
cout << endl;
return 0;
}Não é imediato que este código faz o proposto, mas se o estudarem (e executarem) verão que faz.
A pergunta pertinente a fazer agora é: como depende o tempo de
execução deste algoritmo em relação ao tamanho da sequência, $n$?
Supondo que leram a secção anterior e o artigo sobre análise de
algoritmos, não deve ser
difícil ver que executamos a linha if (seq[j] < seq[mposicao])
exatamente $n + (n - 1) + \ldots + 1$ vezes e que esta linha é a que
domina o tempo de execução. Isto é exatamente $\frac{n(n + 1)}{2}$, o
que significa que, usando a notação do artigo de análise de
algoritmos, este algoritmo tem uma complexidade temporal de $O(n^2)$.
Este algoritmo que descrevemos é conhecido como selection sort, pois ordena selecionando em cada iteração o mínimo da subsequência que ainda temos de ordenar. Para mais informações sobre este algoritmo recomendamos a página da wikipédia.
Como vimos, este algoritmo tem um tempo de execução de $O(n^2)$, daqui a pouco veremos como (com algum trabalho) fazer um algoritmo com tempo de execução $O(n \log n)$. Para quem não conhece, $\log$ refere-se ao logaritmo, o artigo nove introduz este conceito.
Aplicações de ordenação
Ordenar uma sequência parece uma tarefa importante, mas porquê? Na realidade há imensas situações onde ordenar uma sequência nos pode ajudar a extrair alguma informação dessa sequência. Vamos ver uma muito importante numa secção futura, mas para já vamos ver um exemplo mais simples. Considerem o seguinte problema:
A coleção de cromos de jogadores e figuras do mítico clube de futebol Salgueiros é a mais importante e cobiçada da juventude hoje em dia. Há um total de N cromos para colecionar, sendo que cada cromo tem associado um número de 1 a N que é único a esse cromo. O Pedro tem uma coleção de M cromos, alguns possivelmente repetidos, e quer saber quantos cromos lhe falta para terminar a coleção, consegues ajudá-lo?
Neste problema recebemos um conjunto de M números entre 1 a N e queremos saber quantos números de 1 a N faltam a esse conjunto. Por exemplo, se N = 4 e M = 6 e o conjunto de números for 4, 3, 1, 1, 4, 4, então apenas o número 2 está em falta. Fazemos aqui uma pequena nota, para perceber o enunciado de um problema por vezes ajuda olhar para casos simples (como os casos de exemplo) e resolver manualmente para garantir que percebemos o que é pedido.
Vamos descrever dois algoritmos diferentes que resolvem este problema:
Ideia 1
O algoritmo mais simples que resolve este problema consiste em passar por cada número um a um e verificar se já o vimos anteriormente. Com dois ciclos for a implementação fica muito simples. Usando a nossa notação de analisar tempos de execução, este algoritmo é um algoritmo $O(M^2)$, visto que para cada elemento da sequência tem de passar pela sequência toda.
Ideia 2
Comecemos por supor que a sequência de números está ordenada. Nesse caso para um dado número da sequência é fácil de ver se é repetido ou não: basta ver se o número é igual ao número anterior da sequência. Isto apenas necessita de uma passagem pela sequência, ou seja, tem um tempo de execução $O(M)$. Claro que isto apenas se verifica se a sequência estiver ordenada, se não teremos de a ordenar, o que com o nosso algoritmo anterior implica que este algoritmo seria $O(M^2)$. Porém, como foi mencionado vamos ver um algoritmo com tempo de execução $O(N \log N)$, o que é bastante melhor!
Recursividade
Antes de continuarmos com algoritmos de ordenação vamos ver um conceito de programação muito importante e que nos será útil para o resto deste artigo. Recursividade é a ideia de uma função se chamar a si própria, mas mais que isso, é a ideia de resolver um problema ao resolver instâncias mais pequenas do mesmo problema. Veremos como aplicar esta ideia a ordenação em breve, mas vamos ver um exemplo para a motivar primeiro.
A sequência de Fibonacci é uma conhecida sequência de números que segue a seguinte regra: os primeiros dois elementos são ambos 1; os restantes elementos são sempre a soma dos dois anteriores. Ou seja, a sequência começa com 1, 1, 2, 3, 5, 8, 13, 21, 34, ... Uma maneira mais formal de definir esta sequência é: $F_0 = 1, F_1 = 1, F_i = F_{i - 1} + F_{i - 2}$, onde $F_i$ representa o $i$-ésimo número da sequência. Vamos implementar uma função que calcula o $i$-ésimo número da sequência de Fibonacci da seguinte forma:
int fibonacci(int i) {
if (i == 0 || i == 1)
return 1;
else
return fibonacci(i - 1) + fibonacci(i - 2);
}A própria definição de um número desta sequência depende de si própria. Reparem que este programa pode ser dividido em duas partes: um caso base, ou seja, um conjunto de valores para os quais sabemos a solução (neste caso sabemos que os primeiros dois números da sequência são 1); um caso recursivo, onde definimos o seu valor em relação a instâncias mais pequenas. O caso base é importante, caso contrário o programa nunca teria fim! Quando resolvemos um problema de carácter recursivo é preciso ter atenção ao caso base e garantir que este defina a solução de todos os outros casos, o que é uma forma de dizer garantir que não temos nenhum caso recursivo que só dependa de outros casos recursivos (neste caso o programa entraria em ciclo e nunca terminaria).
De notar que esta não é a melhor forma de calcular números de Fibonacci (pensem porquê), mas é um exemplo instrutivo de recursividade.
Ordenar eficientemente
O algoritmo de ordenação que esta secção explica é o mais complexo até agora e é o primeiro algoritmo que requer algum tempo para pensar porque funciona e como. De notar que existem imensos algoritmos de ordenação (muitos mesmo), mas só iremos abordar um aqui, que é conhecido como merge sort.
Considerem o seguinte subproblema mais simples: são nos dadas duas sequências de números, ambas ordenadas, e queremos determinar a sequência ordenada da junção das duas. Por exemplo, imaginem que temos a sequência $3, 5, 5, 7$ e a sequência $1, 2, 4, 6, 7$, queremos juntar as duas e obter a sequência resultante ordenada, o que seria $1, 2, 3, 4, 5, 5, 6, 7, 7$. Uma solução possível seria simplesmente juntar as duas sequências e usar o nosso algoritmo de ordenação anterior para obter a sequência resultante ordenada, mas isso seria $O(N^2)$, o nosso objetivo será fazer isto em tempo $O(N)$, onde $N$ é o tamanho das duas sequências (vamos supor que têm o mesmo tamanho para simplificar).
Aqui será útil revisitar a analogia do baralho de cartas: suponhamos que temos dois baralhos com $N$ cartas cada, ambos ordenados. Queremos juntar os dois e obter o baralho resultante ordenado. Podemos fazer o seguinte: começamos por olhar para a carta no topo de cada baralho; a menor das duas será a primeira carta do baralho resultante, por isso podemos tirá-la do seu baralho e começar a construir o baralho resultante. Agora fazemos a mesma coisa: olhamos para a carta no topo dos dois baralhos e escolhemos a menor para o baralho resultante. Repetimos isto até esgotar ambos os baralhos. A imagem animada seguinte representa este mesmo processo para as sequências $1, 3, 6$ e $2, 4, 5$.
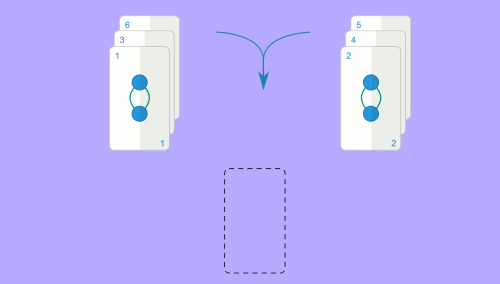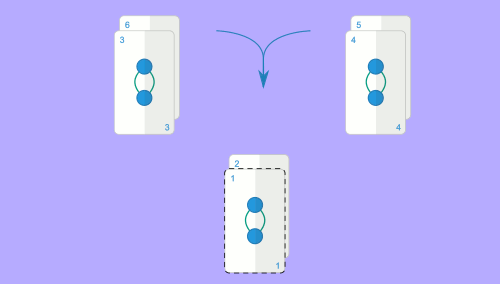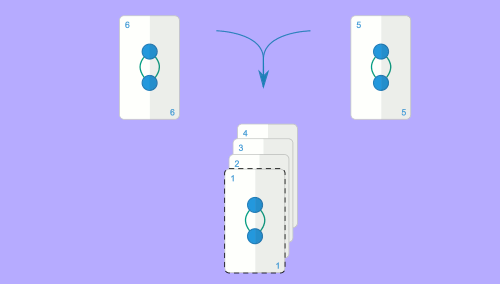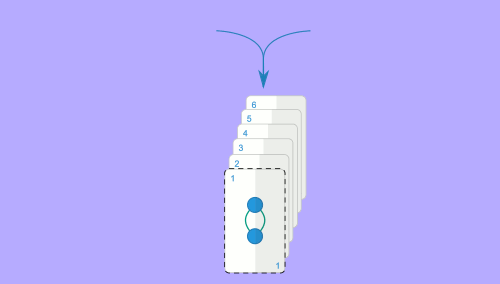
Este algoritmo é claramente $O(N)$, visto que percorremos as duas sequências uma única vez para construir a sequência resultante. Para referência, este método chama-se merge e é o que dá o nome ao algoritmo de ordenação mencionado. A implementação deste método requer algum cuidado, mas não é muito difícil:
#include <iostream>
using namespace std;
int seq1[100]; // Array sequencia 1
int seq2[100]; // Array sequencia 2
int seq[200]; // Array sequencia resultante
int main() {
int n;
cin >> n;
// Assumimos que a sequencia esta ordenada
for (int i = 0; i < n; i++) // Ler a sequencia 1
cin >> seq1[i];
// Assumimos que a sequencia esta ordenada
for (int i = 0; i < n; i++) // Ler a sequencia 2
cin >> seq2[i];
int i1 = 0, i2 = 0; // Iteradores das sequencias, "topo" dos baralhos
int is = 0; // Iterador da sequencia resultante
while (i1 < n || i2 < n) {
// Se ainda ha elementos no primeiro baralho e ou o segundo baralho
// esta vazio ou a carta menor e do primeiro baralho
if (i1 != n && (i2 == n || seq1[i1] <= seq2[i2])) {
seq[is] = seq1[i1]; // Copia a carta do primeiro baralho
is++;
i1++;
}
else {
seq[is] = seq2[i2]; // Copia a carta do segundo baralho
is++;
i2++;
}
}
for (int i = 0; i < 2 * n; i++) // Imprimir a sequencia
cout << seq[i] << " ";
cout << endl;
return 0;
}Vamos agora voltar ao problema original de ordenar uma sequência de números. A ideia do algoritmo completo é a seguinte: vamos ordenar a primeira metade da sequência e a segunda metade da sequência independentemente uma da outra. Tendo as duas ordenadas, estamos na situação que acabámos de ver como resolver, basta aplicar o nosso método merge. Mas como é que podemos ordenar as duas metades eficientemente se não sabemos ordenar a sequência completa? Rescursividade! Usamos o mesmo método que tinhamos para ordenar a sequência completa! Qual é o nosso caso base? É quando a sequência a ordenar tem apenas um elemento.
Porque é que este algoritmo é $O(N\log N)$? Antes de responder a esta pergunta, convém estudar implementação deste algoritmo, para garantir que perceberam a ideia. Na realidade a implementação é muito simples, o trabalho principal é feito pelo algoritmo merge que já fizemos há pouco, mas vamos rescrever este método como uma função e escrever uma função para ordenar uma sequência. A nossa função de ordenação receberá 3 parâmetros: uma array a ordenar; um limite inferior do intervalo da array a ordenar; um limite superior do intervalo da array a ordenar. Os limites do intervalo indicam que queremos ordenar a array nesse intervalo, isto para podermos ordenar os diferentes pedaços (metades de metades) que o merge sort ordena e depois junta usando a função merge. Notem ainda que em C++ as arrays são passadas por referência como argumentos de funções, ou seja, ao modificarmos a array do primeiro parâmetro estamos a modificar a array original, que é outra forma de dizer que a array não é copiada. Na função merge alterada vamos começar por copiar os intervalos de valores relevantes da array original para duas arrays auxiliares e depois aplicar exatamente o mesmo programa que fizemos anteriormente. Vamos ainda generalizar ligeiramente o programa anterior para aceitar arrays de tamanhos distintos (se o comprimento a ordenar for impar temos de juntar arrays de tamanhos diferentes, não dá para obter metades exatamente iguais).
#include <iostream>
using namespace std;
int seq[100]; // Array para guardar a sequencia
int seq1[100]; // Array auxiliar para a funcao merge
int seq2[100]; // Array auxiliar para a funcao merge
void merge(int arr[100], int l, int m, int r) {
int n1 = 0; // Tamanho da primeira metade
for (int i = l; i <= m; i++) { // Copiar a primeira metade
seq1[n1] = arr[i];
n1++;
}
int n2 = 0; // Tamanho da segunda metade
for (int i = m + 1; i <= r; i++) { // Copiar a segunda metade
seq2[n2] = arr[i];
n2++;
}
int i1 = 0, i2 = 0; // Iteradores das sequencias, o "topo" dos baralhos
int is = l; // Iterador da sequencia resultante
while (i1 < n1 || i2 < n2) {
if (i1 != n1 && (i2 == n2 || seq1[i1] <= seq2[i2])) {
arr[is] = seq1[i1];
is++;
i1++;
}
else {
arr[is] = seq2[i2];
is++;
i2++;
}
}
}
void mergesort(int arr[100], int l, int r) {
if (l == r)
return;
int m = (r + l) / 2; // Obter o ponto do meio do intervalo [l, r]
mergesort(arr, l, m); // Ordenar a primeira metade
mergesort(arr, m + 1, r); // Ordenar a segunda metade
merge(arr, l, m, r); // Juntar!
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) // Ler a sequencia
cin >> seq[i];
mergesort(seq, 0, n - 1);
for (int i = 0; i < n; i++) // Imprimir a sequencia
cout << seq[i] << " ";
cout << endl;
return 0;
}Porque é que este algoritmo corre em tempo $O(N \log N)$? Ora, vamos analisar a árvore recursiva do algoritmo, ou seja, a hierarquia de chamadas recursivas efetuadas pelo algoritmo. A imagem seguinte mostra a árvore recursiva para a sequência $6, 3, 1, 2, 5, 4$ (as setas direitas representam chamadas recursivas e as setas encaracoladas junções/merges):
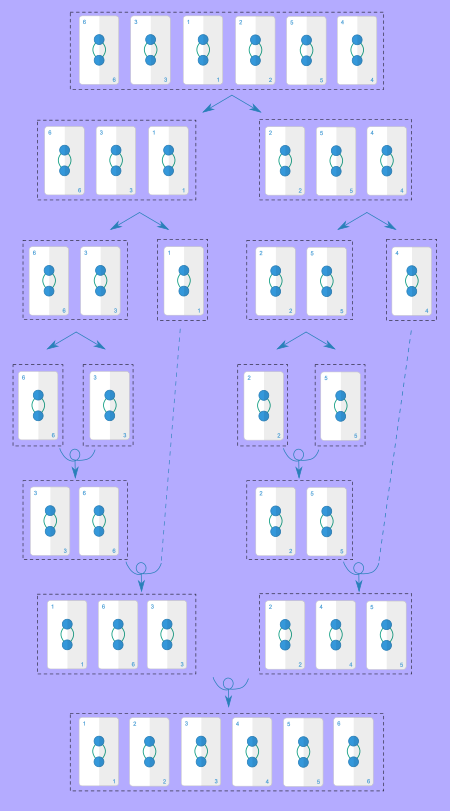
A cada nível da nossa recursão (que equivale a cada nível precedido por setas direitas na imagem a cima) duplicamos o número de sequências a ordenar, mas o tamanho de cada uma é dividido em metade. Adicionalmente, fazemos um total de $O(N)$ operações por nível, ao somarmos as operações que temos de fazer para cada junção para cada sequência a ordenar. Notem que é $O(N)$ total por nível e não por cada sequência, pois o tempo de execução da operação merge depende do tamanho das sequências a juntar. Isto significa que o tempo de execução vai depender da altura da árvore de recursão. A árvore de recursão continua a aumentar até o tamanho de cada sequência ser 1, mas por cada nível dividimos o tamanho de cada sequência por 2. Isto significa que a altura da árvore é o número de vezes que podemos dividir $N$ por 2 até obtermos um valor igual a 1. Isto corresponde exatamente ao logarítmo de $N$ de base 2! Uma forma de vermos isto é representarmos por $a$ a altura da árvore de recursão, sabemos que vamos dividir $N$ por 2 $a$ vezes, ou seja, dividimos por $2^a$, e obtemos 1, isto é: $N / 2^a = 1$ ou seja $N = 2^a$, o que significa que $a$ é o logarítmo de base 2 de $N$, por definição! Isto implica que o nosso algoritmo corre em tempo $O(N\log N)$, temos $\log N$ níveis e em cada nível fazemos $O(N)$ operações no total.
Agora já têm todas as ferramentas para resolver eficientemente o problema do início deste artigo!

Problema G: A coleção do Pedro
Este problema está disponível no Mooshak de treino como o problema G
Pesquisa em listas
Vamos passar a um tópico diferente e ver um algoritmo novo, nomeadamente de pesquisa em listas. Considerem que têm uma sequência de $N$ números e querem saber se essa sequência incluí o número 5. Bom, já deve ser imediato ver que apenas precisamos de percorrer a lista e verificar um a um se cada elemento é ou não 5. Isto, claramente, tem um tempo de execução $O(N)$. E se quisermos fazer melhor? Parece óbvio ver que é impossível, visto que pode existir um 5 em qualquer parte da sequência e não podemos ter a certeza que não existe um 5 sem olhar para todos os elementos. Mas e se a sequência tiver ordenada?
Como sempre estar ordenado ajuda-nos imenso. Vamos supor que temos uma sequência ordenada com 1000 números e queremos saber se o número 314 está contido nela. Começemos por tentar adivinhar uma posição onde o número possa estar, por exemplo a posição 500. Olhamos para o número da sequência na posição 500 e observamos que é o número 425. Visto que a sequência está ordenada, sabemos que nenhum elemento nas posições de 500 a 1000 pode ter o número 314. Agora vamos olhar para o elemento na posição 250 e verificamos que é o número 300. Isto significa que nenhum elemento entre 1 e 250 pode ser o 314.
Qual é a ideia do método anterior? Manter um intervalo de posições onde possa estar o valor que pretendemos. Verificamos o elemento do meio do intervalo. Se for maior que o elemento que pretendemos, eliminamos a metade direita do intervalo, se for menor a metade esquerda, se for o próprio elemento encontrámos o que pretendiamos. Repetimos isto até o intervalo ficar vazio. Qual é o tempo de execução deste algoritmo? De cada vez que olhamos para um número da sequência eliminamos pelo menos metade do intervalo de valores e paramos quando o intervalo ficar vazio. Isto tem exatamente o mesmo comportamento que o exemplo anterior da árvore de recursão, ou seja, no total olhamos para $O(\log N)$ elementos. Isto é uma melhoria enorme em relação a procurar numa lista não ordenada! Este método é conhecido como pesquisa binária e é dos algoritmos mais fundamentais. A implementação deste algoritmo também é muito simples:
#include <iostream>
using namespace std;
int seq[100];
int pesquisabinaria(int arr[100], int n, int q) {
int l = 0, h = n - 1; // Os limites do intervalo de posicoes possiveis
// inicialmente [0, n - 1]
while (l <= h) { // Enquanto o intervalo não for vazio
int m = (l + h) / 2; // Obter o elemento do meio do intervalo
if (seq[m] == q) // Se encontramos o elemento
return 1;
else if (seq[m] < q) // Se o elemento e menor cortamos o intervalo
l = m + 1;
else // Se o elemento e maior cortamos o intervalo
h = m - 1;
}
return 0; // Nao encontramos
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) // Ler a sequencia
cin >> seq[i];
int q;
cin >> q; // O numero a pesquisar
cout << pesquisabinaria(seq, n, q) << endl;
return 0;
}Este método tem aplicações para além de pesquisa em listas, por exemplo se a lista for de certa forma implícita. Não iremos abordar esse tema neste conjunto de artigos introdutórios, mas é um dos primeiros tópicos que devem explorar depois de terminarem estes artigos. O último artigo contém algumas dicas sobre como continuar a aprender, quase todas as referências dadas incluiem uma discussão mais detalhada sobre pesquisa binária.
Aplicações de pesquisa binária em listas
Para terminar este longo artigo, vamos tentar aplicar esta ideia num problema.
Para surpreender a sua família no Natal, o Guilherme decidiu comprar um conjunto de presentes. Depois de fazer uma pesquisa, encontrou $N$ presentes que lhe interessam comprar e apontou o preço de cada um. O Guilherme quer comprar o máximo número de presentes possível, mas infelizmente tem um orçamento limitado. Para saber de quanto dinheiro precisa, o Guilherme tem $M$ orçamentos diferentes e quer saber o máximo número de presentes que consegue comprar com cada um.
Este problema não é uma aplicação direta de pesquisa binária, temos de pensar um pouco primeiro. Vamos focar-nos num único orçamento e ver como calcular eficientemente o máximo número de presentes que o Guilherme consegue comprar e depois repetir o mesmo processo para cada um dos $M$ orçamentos. Vamos supor que temos um orçamento de $X$ euros e queremos comprar o máximo número de presentes com esse valor. Não é difícil de observar que o ideal é comprar primeiro os presentes mais baratos, visto que apenas nos interessa o número de presentes que compramos. Por isso, podemos começar por ordenar a lista de preços assumindo que compramos sempre um prefixo da lista de preços ordenada (ou seja, um conjunto contíguo dos primeiros preços). Agora só temos de encontrar o maior prefixo cuja soma seja menor ou igual ao nosso orçamento.
Vamos ver um exemplo, suponhamos que os preços ordenados são $1, 3, 5, 5, 6, 8$. Temos sempre de escolher um prefixo, por isso podemos calular logo as somas de todos os prefixos, ou seja, podemos guardar numa array a soma do primeiro elemento, dos primeiros dois elementos, etc. Neste caso essa array seria $1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 + 5, 1 + 3 + 5 + 5 + 6, 1 + 3 + 5 + 5 + 6 + 8$ que corresponde a $1, 4, 9, 14, 20, 28$. Agora o a única coisa que temos de fazer é encontrar o maior elemento desta array que é menor ou igual a $X$. Notem que se tivessemos que encontrar um elemento exatamente igual a $X$ então o problema estaria resolvido em $O(\log N)$: esta array de $N$ elementos está claramente ordenada por ordem crescente, por isso só precisariamos de usar o nosso algoritmo de pesquisa binária. Porém, podemos na mesma aplicar o nosso algoritmo de pesquisa binária ao caso em que queremos o maior elemento que é menor ou igual a $X$, apenas teremos de modificá-la ligeiramente.
Para modificar a pesquisa binária temos de modificar o seguinte. No algoritmo original ao compararmos o elemento do meio com $X$, se este for menor que o elemento que pretendemos eliminamos a metade esquerda do intervalo. No algoritmo modificado, se este for menor ou igual ao elemento que pretendemos eliminamos a metade esquerda do intervalo exceto o próprio elemento do meio. Não é difícil agora acertar os detalhes e ter este algoritmo a funcionar, mas é preciso algum cuidado (pensem com calma no algoritmo enquanto implementam).
Como sempre, podem submeter este problema no Mooshak.

Problema H: O Guilherme vai às compras
Este problema está disponível no Mooshak de treino como o problema H
Nota final
Terminamos por aqui este artigo de introdução a algoritmos. Notamos que há muita informação neste artigo e por isso pode levar algum tempo a assimilar tudo. A ideia de recursividade que foi apenas mencionada aqui é muito poderosa e pode simplificar imenso alguns problemas. Por exemplo, imaginem que queriamos determinar uma lista de todo os conjuntos de inteiros positivos cuja soma é exatamente $X$ (notem que este valor cresce exponencialmente, ou seja, para valores altos de $X$ há mesmo muitos conjuntos). Por exemplo, para $X = 3$ temos os conjuntos $\{3\}, \{1, 2\}, \{1, 1, 1\}$. A observação importante aqui é: se incluirmos o valor 1 inicialmente na nossa lista, agora só temos de determinar todos os conjuntos de inteiros positivos cuja soma é 2 e posteriormente juntar-lhe o elemento 1.
No próximo artigo iremos falar de um tema ligeiramente diferente mas também muito importante para resolver problemas algorítmicos.