Introdução à Análise de Algoritmos
Algoritmos são a moeda da programação competitiva (e da programação em geral também). É através deles que se resolvem problemas. Como tal, é necessário saber quanto valem, ou seja, é preciso saber o quão eficientes são. A importância de avaliar um algoritmo ultrapassa a mera curiosidade. Na verdade é muito útil durante uma prova pois permite-nos saber quantos pontos terá a nossa solução para um determinado problema além de nos permitir comparar duas soluções diferentes e saber qual a melhor a usar. Assim, já temos uma razão mais que válida para aprender a analisar os nossos algoritmos.
O que é a Eficiência de um Algoritmo
A eficiência de um algoritmo está relacionada com o seu comportamento mediante um crescimento no tamanho dos dados que processa. Para avaliar esse comportamento é preciso medir vários parâmetros relacionados com a sua execução. Os dois parâmetros mais importantes são a memória e o tempo, que correspondem aos recursos de memória que o algoritmo requer e ao tempo que ele leva a correr. Para perceber qual a importância de cada parâmetro recorre-se ao parâmetro mais restrito, o que em termos técnicos se denomina de "bottleneck". O objetivo é perceber qual o parâmetro que, de acordo com os recursos disponíveis, impede que o algoritmo termine corretamente. Por exemplo, se para um conjunto determinado de dados a processar, um algoritmo necessite de 1 dia para terminar mas apenas 1MB de memória, o parâmetro mais restritivo será o do tempo (pois uma máquina minimamente decente nos padrões atuais tem muito mais que 1MB de memória, mas nós não temos um dia para o algoritmo correr, especialmente se for durante um concurso). A avaliação destes parâmetros chama-se normalmente de complexidade segundo um parâmetro do algoritmo (por exemplo, a complexidade temporal é a medida de tempo que quantifica o algoritmo).
Notem que a memória e o tempo não são os únicos possíveis parâmetros a avaliar. Apesar de o parâmetro mais usado (especialmente em ONI) ser o tempo, na IOI há cada vez mais problemas que recorrem a outro tipo de limites (como um número máximo de chamadas de uma determinada função), é importante perceber de antemão quais são os parâmetros importantes do problema.
Sabendo isto, falta saber como medir a eficiência segundo um certo parâmetro. Poderíamos fazer esta análise por vários pontos de vista, mas para simplificar e também porque é o caso mais comum, utilizaremos a medida do tempo. A questão agora é então: como medir o tempo que um algoritmo demorará a correr para um certo conjunto de dados. Primeiro que tudo é importante reparar que é difícil, senão impossível, medir exatamente o tempo que um algoritmo demorará. Por isso é preciso relaxar um pouco o problema, ou seja, assumir algumas coisas.
Medir a Eficiência
Vamos considerar que temos um certo problema e chegámos a um algoritmo que resolve esse problema, mas queremos saber quanto demora para um determinado caso de teste. Sabemos que o input (os dados a processar), são $N$ elementos de um certo tipo ($N$ inteiros por exemplo ou $N$ strings). É certo que executar uma operação (uma adição, uma atribuição a uma variável, um acesso à memória através de um array) demora um certo tempo a ser feita, por isso qualquer medida de tempo será relativa ao número de operações feitas vezes o tempo que cada uma demora a ser feita. E pronto, está feito, sabemos medir o tempo que um algoritmo demora a correr! Mmmm, não propriamente...
Levanta-se agora uma questão importante: como estimar o número de operações que um algoritmo faz? Reparem na minha escolha de palavras: estimar, é importante perceber que calcular exatamente o número de operações que um algoritmo faz é extremamente difícil e imprático durante um concurso (e às vezes até fora). Por isso o objetivo é ter uma ideia que nos permita avaliar como se comportará o nosso algoritmo com alguma precisão. Bom, passemos a um caso prático e analisemos um algoritmo.
Utilizando a notação que introduzimos há dois parágrafos atrás, vamos resolver um problema muito simples: são dados $N$ números inteiros positivos ($N$ é obviamente maior que 0) e é nos pedido que retornemos o maior deles. Super fácil, não é? Como eu sou simpático, segue um pequeno código em C/C++ que resolve este problema (apenas a parte "relevante"):
int N, i;
scanf("%d", &N);
int mx = 0; // 1 operação
while (i < N) // 1 operação
{
int num;
scanf("%d", &num);
if (num > mx) // 1 operação
mx = num; // 1 operação
i = i + 1; // 2 operações
}
printf("%d\n", mx);Nada de complexo espero (notem que utilizei um while em vez de um for para facilitar a análise). Para simplificar as nossas contas vamos ignorar as funções de input/output e consideremos apenas o resto das operações. Os comentários indicam o número de operações por linha. A primeira coisa que podemos notar é que a linha mx = num; nem sempre é executada, só o é se o if da linha anterior o deixar. Logo temos aqui um problema para resolver.
Muitos algoritmos têm um comportamento que depende dos dados que processam, até os mais simples como o acima. Como tal não é possível ter uma fórmula exata que se adeque a todos os inputs possíveis. Assim, temos de arranjar uma estratégia alternativa. Podemos medir o tempo médio, mas este além de ser difícil de calcular, num concurso não ajuda muito pois podem haver casos de teste que demorem mais que o médio e em que por isso o algoritmo falha. Podemos medir o melhor tempo possível, mas ser otimista também não nos ajuda pela mesma razão que o caso médio. Falta então olhar para o pior caso. Com efeito, olhar para o maior tempo que o nosso algoritmo demoraria é uma boa ideia pois dá-nos um limite superior para o tempo que o algoritmo demorará a correr. Se para o tamanho máximo o nosso algoritmo demorá no pior caso um tempo razoável, então demorará para todos os tamanhos possíveis.
Podemos agora voltar à nossa análise fazer mais uma observação: todas as operações dentro do while são executadas $N$ vezes. Agora então se quisermos obter uma fórmula que descreva quantas operações o nosso algoritmo faz no pior caso chegaremos à seguinte expressão: $1 + 1N + 1N + 1N + 2N = 1 + 5N$. Já é uma expressão relativamente simples, mas podemos fazer ainda melhor.
Notação e Análise Assintótica
Primeiro que tudo vamos considerar uma expressão diferente: $3N + N^2$. Se fizermos as contas para $N = 5$ temos que o resultado é $40$. Mas se fizermos para $N = 1,000$, temos $1,003,000$. Embora parecendo que voltámos à escola primária, há uma diferença importante nos dois cálculos (além do resultado). No primeiro caso, $3 \times 5$ é aproximadamente igual a $5^2$. Porém no segundo, $3 \times 1.000$ é muito mais pequeno do que $1.000^2$. E quanto maior for o $N$ maior será a diferença entre eles. Isto tudo para chegar à conclusão que é importante ver qual é o termo na expressão do número de operações que "domina", ou seja, que à medida que $N$ cresce, esse termo é o que sofre uma mudança maior (para aqueles que conhecem limites, a ideia é ver qual o termo que cresce até infinito mais depressa). Para as expressões mais simples é fácil de ver qual é o termo: é o termo que tem o maior grau de $N$ (o que nesta expressão é claramente o termo de grau 2, $N^2$).
Voltando então à nossa análise do algoritmo acima (do código dado), claramente o maior termo da expressão que obtivemos é $5N$. E vou argumentar que ainda podemos simplificar mais esta expressão (??!). E para isso vou recorrer a uma notação muito usada (e para quem já leu alguma solução de problemas de ONI ou IOI já a viu de certeza) chamada Big-O Notation. A ideia desta notação é definir um limite superior a uma função de acordo com a taxa de crescimento da função. Assim, por exemplo, se tivermos uma função como $5N$, podemos dizer que $5N = O(N)$. A razão é simples, visto que estamos a falar em taxa de crescimento da função, qualquer que seja a constante que multiplique $N$, à medida que $N$ cresce, esta vai perdendo importância em relação ao fator dominante $N$. É claro que o fator continuaria a ter uma importância, embora pequena, no tempo que o algoritmo demoraria a correr, mas além de permitir comparar algoritmos com crescimentos semelhantes podemos pensar que se um algoritmo demorar 5 ou 10 segundos a correr não é tão drástico como demorar 5 segundos ou 5 dias. É importante notar que a notação Big-O impõe um limite superior, por isso, tecnicamente $3N = O(N^3)$, porém, este limite superior não nos revela o crescimento real da função, por isso faz muito mais sentido dizer que $3N = O(N)$. Assim evita-se usar notações e ferramentas mais complexas e também mais suscetíveis a confusão, mas através de uma alternativa que nos permite perceber o que precisamos para analisar o algoritmo. Outra vantagem que isto nos dá é podermos definir complexidade.
Para melhorar o entendimento desta notação, podemos usar alguns exemplos de funções. Primeiro temos: $7N^2 = O(N^2)$, pois claramente o termo dominante aqui é o $N^2$ enquanto que o 7 é apenas uma constante. Segundo: $2N^2 + N^3 = O(N^3)$, este caso é semelhante ao anterior, aqui o termo com o maior expoente é o $N^3$, logo é o termo dominante. Finalmente temos: $O(N) + O(N) = O(N)$, isto vem de: $O(N) + O(N) = O(2N) = O(N)$.
Complexidade Exponencial e Polinomial
Notem que nem todas as funções serão da forma $N^C$ (onde $C$ é uma constante). Podemos distinguir duas classes de funções muito distintas: as polinomiais e as exponenciais. As exponenciais são da forma $C^N$ (onde $C$ pode ser uma constante ou $N$). Não é muito óbvio à primeira vista, mas estas funções são as que têm o maior crescimento. Na verdade, este crescimento é muito maior que o das funções polinomiais. Uma experiência simples de se fazer é pegar numa calculadora e começar com o número $2$ e multiplicá-lo por $2$ e depois multiplicar o resultado por $2$ várias vezes (que é o equivalente a fazer $2^C$) e ver quantas vezes é preciso fazer isto para que o resultado seja maior que um milhão. O resultado é apenas $20$, enquanto que se quiséssemos encontrar o número mais pequeno tal que o seu quadrado fosse maior que um milhão, teríamos de chegar até ao $1,000$! Em contraste com as funções exponenciais estão todas as funções onde o $N$ não está em expoente. Isto inclui funções um bocadinho mais avançadas (mas nada de especial) como a função logaritmo. Um logaritmo é o contrário de uma exponencial (é o número a que temos de elevar a base do logaritmo para dar outro valor fixo), por isso podemos pensar que ao contrário das exponenciais, o crescimento do logaritmo é muito pequeno (o logaritmo de base $2$ de um milhão é apenas cerca de $20$!). Para mais informações sobre logaritmos o melhor é mesmo ver a Wikipedia.
Estamos agora a aproximar-nos da definição que dei há pouco de complexidade. A complexidade temporal de um algoritmo pode então ser definida como o limite superior do número de operações feitas do algoritmo, ou seja, é o $O()$ dessa expressão! Podemos assim concluir que para analisarmos a complexidade temporal do algoritmo basta chegar à expressão $O()$ que o quantifica. Mas faltam-nos duas habilidades importantes: perceber o que significa uma expressão e saber calculá-la.
Intuição
Para terminar a discussão teórica de notação Big-O vamos só fazer uma pausa e refletir (brevemente) sobre o que significa isto.
Antes de mais só uma nota rápida. A notação de Big-O pode ser usada para comparar quaisquer funções. Por exemplo, podemos dizer que $4N = O(3N^2)$, conseguimos ver que a segunda função limita a primeira superiormente, por isso é válido escrever isso. É mais útil quando estamos a descrever a complexidade de um algoritmo "despir" as fórmulas de constantes para podermos passar a ideia geral, mas é importante perceber que a notação é mais flexível do que isso e em alguns casos (possivelmente fora de concursos) pode ser útil.
Agora por uma questão de completude, vou apenas definir um bocadinho mais matematicamente o que significa ser $O()$ de alguma coisa. Isto não é essencial pois na maioria dos casos (como já vamos ver) os resultados são de uma forma simples (em concursos), mas ajuda a perceber exatamente o que significa. Ora então, dizer que uma função $f(N)$ é $O()$ de uma função $g(N)$, escreve-se: $f(N) = O(g(N))$ é o mesmo que dizer que existe um valor real $c$ tal que $f(N) <= c \times g(N)$ , para valores de $N$ a partir de um certo ponto fixo (que podemos chamar de $N_0$). A imagem seguinte ilustra isto (para $f(N) = 5N + 100$, $g(N) = N^2 + 5$, $c = 2$):
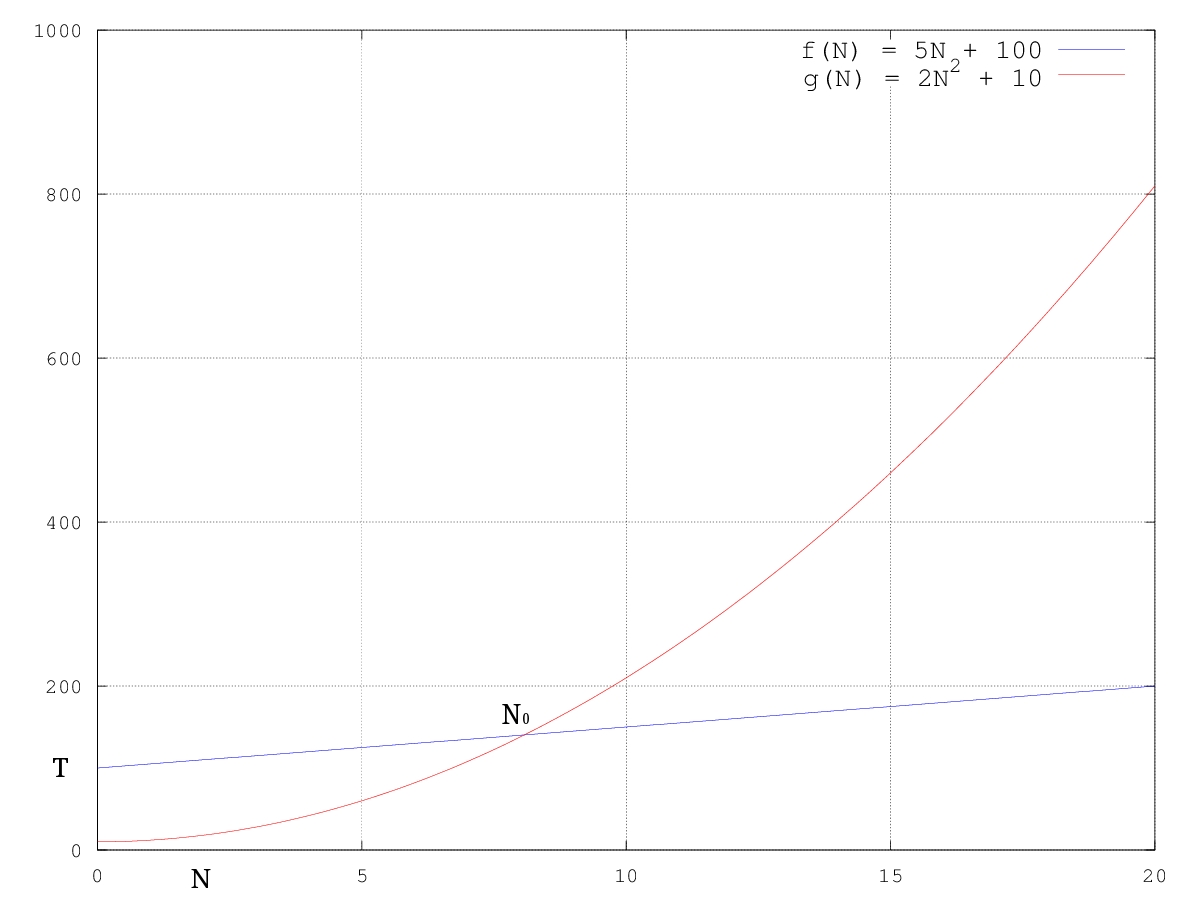
Conseguimos ver que: $5N + 100 = O(N^2 + 5)$ pela imagem, já que a partir do ponto $N_0$ a segunda função é sempre maior que a primeira. Podemos provar isto formalmente (matematicamente), mas não é necessário para concursos (novamente, para quem sabe limites é muito fácil, mas mesmo não conhecendo é possivel ao estabelecer desigualdades até provar que $5N + 100 <= 2N^2 + 10$ para $N$ superior a $10$ por exemplo). O objetivo é ter uma ideia de como se comportam as funções e é fácil de ver (tanto pela imagem como pensando) que a partir de $N_0$, $2N^2 + 10$ será sempre maior que $5N + 100$.
Cálculo
Vamos agora à parte que esperávamos: calcular a complexidade de algoritmos. Já temos todas as ferramentas necessárias para o fazer e inclusive já o começámos a fazer para o algoritmo acima.
Para o exemplo acima chegámos à conclusão que o algoritmo corria em $O(N)$ contando o número de operações. Porém, fazer este processo repetidamente para cada algoritmo pode ser doloroso, por isso vamos recorrer a algumas observações úteis. A primeira coisa a olhar é o número de ciclos encadeados (para o caso de a expressão ser desconhecida, encadeados significa um dentro do outro). Se tivermos, por exemplo, um algoritmo com 2 ciclos encadeados terá uma complexidade de $O(N^2)$ porque para o primeiro ciclo temos $N$ iterações, e em cada iteração fazemos um ciclo que usa $N$ operações, logo (multiplicando o número de operações de cada um), temos uma complexidade de $O(N \times N) = O(N^2)$.
Daqui podemos generalizar e dizer que um algoritmo que tenha como máximo de ciclos encadeados $C$ (por máximo quero dizer que de todos os ciclos encadeados o maior tem $C$ ciclos, mesmo que haja mais ciclos com tamanhos diferentes menores que $C$, como vimos anteriormente o número de operações que fazem é "dominado" pelos $C$ ciclos encadeados), temos então que a complexidade desse algoritmo é de $O(N^C)$. No exemplo anterior (o código acima), vimos que tem apenas um while sem ciclos encadeados, logo podíamos logo ver que a sua complexidade é de $O(N)$ de acordo com a regra que acabámos de ver.
É uma regra simples, mas não deixa de ser útil. Funciona para muitos casos em concursos e só quando se complica o algoritmo é que será necessário complicar a análise. Não irei falar muito mais de técnicas para analisar algoritmos e de complexidades com fórmulas complicadas (para já). A razão é muito simples visto que analisar algoritmos é uma ferramenta que se desenvolve aprendendo algoritmos. Por isso vão aprender a analisar mais técnicas e mais complexidades enquanto vão aprendendo mais algoritmos (nos próximos artigos claro). Até lá fica a ideia de como funciona, as notações e ferramentas a usar, o que significam e uma leve ideia de como calcular. Já não é mau :)
Aplicação
Para terminar este artigo vamos falar de como aplicar estes conhecimentos num problema. Já discutimos bastante sobre a complexidade temporal e de facto é um tema importante. Mas o objetivo final desta medida é estimar o tempo que demora um algoritmo a correr para perceber quantos pontos receberá (notem que nas ONI o tempo limite por caso de teste é 1 segundo fora problemas excecionais enquanto que na IOI varia de 1 a 10 segundos dependendo do problema). Obviamente que o tempo exato não pode ser calculado e se quisermos ter uma ideia ainda mais precisa de tempo não devemos ignorar as constantes como na notação Big-O. Porém, a notação Big-O já permite uma boa estimativa suficiente para concursos.
Ora então a ideia é, tendo estimado o número de operações, saber, em média, quanto demora uma operação. Obviamente que depende de máquina para máquina mas uma estimativa regularmente usada é que uma operação demora cerca de 10-9 segundos. Assim, a tabela seguinte resume o tempo que algoritmos com diversas complexidades demoram para vários tamanhos de input:
| Complexidade: | $N = 20$ | $N = 100$ | $N = 1000$ | $N = 10000$ |
|---|---|---|---|---|
| $O(\log N)$ | 3 * 10-9 segundos | 7 * 10-9 segundos | 10-8 segundos | 10-7 segundos |
| $O(N)$ | 2 * 10-8 segundos | 10-7 segundos | 10-6 segundos | 10-5 segundos |
| $O(N log N)$ | 6 * 10-8 segundos | 7 * 10-7 segundos | 10-5 segundos | 10-3 segundos |
| $O(N^2)$ | 4 * 10-7 segundos | 10-5 segundos | 10-3 segundos | 0.1 segundos |
| $O(N^3)$ | 8 * 10-6 segundos | 10-3 segundos | 1 segundo | 16 minutos |
| $O(N^4)$ | 2 * 10-4 segundos | 0.1 segundos | 1000 segundos | 115 dias |
| $O(2^N)$ | 10-3 segundos | 1013 anos | 10284 anos | 102993 anos |
| $O(N!)$ | 77 anos | 10141 anos | 102553 anos | 1035642 anos |
Com esta tabela já é possível pegar numa complexidade e nos limites de um problema e ver quantos pontos teria. Agora para diferentes complexidades também não é muito difícil estimar, mas ter ideia de qual a complexidade máxima que um algoritmo tem de ter para passar num determinado tamanho de caso de teste é algo que se deve treinar, por isso passem um tempinho a observar a tabela. Sabendo isto, é possível "adivinhar" em alguns casos qual a complexidade que o nosso algoritmo deve ter, que é uma grande ajuda para completar um problema.
Conclusão
Como nota de despedida falta-me dar umas dicas sobre como aplicar tudo isto com sucesso numa prova.
Primeiro que tudo, devem olhar para os limites (ou restrições) do problema. Se antigamente eram só um conjunto de números que usavam para dar tamanhos a arrays, agora devem olhar para eles com um olhar mais crítico. Sabendo alguma informação da tabela anterior podemos logo (às vezes nem sequer é preciso ler o problema, mas não aconselho nada a fazer isto, primeiro lê-se o problema e só depois os limites) qual a complexidade pedida para cada nível de pontos. Obviamente que não é preciso decorar os tempos individuais para cada complexidade basta saber que normalmente uma operação simples demora 10-9 segundos (o que nos permite fazer estimativas para todo tipo de complexidades) e também que:
- Para $N$ da ordem dos $1,000,000$ ou $100,000$, apenas algoritmos com complexidade $O(N)$ ou $O(N\log(N))$ ou melhor passam.
- Para $N$ da ordem dos $5,000$, apenas algoritmos de complexidade $O(N^2)$ ou melhor passam.
- Para $N$ da ordem dos $300$, apenas algoritmos de complexidade $O(N^3)$ ou melhor passam.
- Para $N$ da ordem dos $80$, apenas algoritmos de complexidade $O(N^4)$ ou melhor passam.
- Para $N$ da ordem dos $20$, apenas algoritmos de complexidade $O(2^N)$ ou melhor passam.
- Para $N$ da ordem dos $10$, apenas algoritmos de complexidade $O(N!)$ ou melhor passam.
Com isto aproveito para notar também que um fator logaritmo é quase sempre irrelevante. Como $\log(1,000,000)$ é mais ou menos $20$ (que é um fator muito pequeno), raramente um problema com complexidade $O(X)$ (sendo $X$ uma função qualquer de $N$) passa mas não $O(X\log(X))$ (mas pode acontecer se os limites forem muito apertados).
Para terminar, é importante que quando estamos a pensar no algoritmo a usar para resolver um problema fazermos este tipo de análise ao mesmo tempo. Só assim é que podemos perceber que um algoritmo que estamos a pensar implementar não vai funcionar para os 100 pontos que todos queremos, mas que se pensarmos um bocadinho melhor chegamos lá.